Эквивалентные разбиения

k-эквивалентное разбиение автомата М называется эквивалентным разбиением М и обозначается 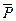, если во всех классах этого разбиения смежные состояния эквивалентны. При этих условиях каждый класс разбиения называется классом эквивалентности. Из материалов § 3.4 следует, что 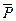является наиболее детальным разбиением P _k. По теореме 3.4, эквивалентное разбиение 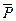может быть получено, если образовывать P _k для k=l, 2, 3... до тех пор, пока первый раз получится разбиение, которое совпадает с предыдущим разбиением. Это разбиение и будет 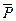. Пусть равенство P _i = P _j означает, что P _i и P _j являются одинаковыми разбиениями, и пусть |P _i | обозначает число классов в P _i. Используя это обозначение, предыдущие результаты могут быть обобщены следующим образом:

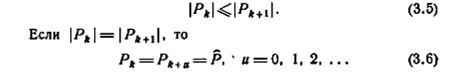
Если все n состояний автомата являются 1-эквивалентными, то разбиение Р₁ состоит из одного класса, содержащего n состояний. Очевидно, что если все n состояний являются 1-эквивалентными, то их первые преемники по отношению к любой входной последовательности являются также 1-эквивалентными. Таким образом, все n состояний должны быть 2-эквивалентными и, следовательно, Р₁ = Р₂. Тогда, по (3.6), Р₁ = 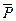и все n состояний являются эквивалентными. Для автомата такого типа f_z (x_v, s_v) является одинаковой для всех sv и, следовательно, f_z (x_v, s_v) = f_z (x_v). Тогда по определению, введенному в § 1.6, можно утверждать, что автомат, в котором все состояния эквивалентны, является тривиальным автоматом. В дальнейшем, если не будет специально оговорено, будут рассматриваться только нетривиальные автоматы, т. е. автоматы, в которых имеется, по крайней мере, одна различимая пара состояний или в 1-эквивалентных разбиениях которых имеется, по крайней мере, два класса.

Лемма 3.8. Если Р _k ≠ Р _k-1, то

|Pk|≥k+1. (3.7)

Доказательство. Если Р _k ≠ Р _k-1 то, по (3.5) и (3.6), |Р _r | > |Р _r-1 | для r = 1. 2,..., k. Поскольку |P₁|≥2, то (3.7) следует по индукции.

Лемма 3.9. Если для автомата с n состояниями Р _k ≠ Р _k-1, то число состояний в каждом классе разбиения Р _k не превышает n - k.

Доказательство. Согласно лемме 3.8, число классов в P _k равно, по крайней мере, k+1. Предположим, что один класс содержит больше чем n - k, скажем n — k + 1 состояний. Тогда, поскольку каждый другой класс в P _k должен содержать, по крайней мере, одно состояние, общее число состояний в Pk будет не менее k + (n — k + 1) = n + 1. Лемма доказана, так как общее число состояний не может превосходить n.

Лемма 3.10. Для автомата с n состояниями Р_n = Р _n-1

Доказательство. Если Р _n ≠ Р _n-1, то, согласно лемме 3.8, | Р_n | ≥ n+1 Так как число классов в k-эквивалентном разбиении автомата с n состояниями не может превышать n, то полученное противоречие доказывает лемму. Из леммы 3.10 и уравнения (3.6) можно вывести следующее заключение:

Теорема 3.5. Для автомата с n состояниями

P _n-1 = 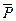. (3.8)

Таким образом, процесс определения 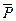для автомата с n состояниями путем последовательного построения Р _k для k = 1, 2, 3 требует не более n—1 построений.

Другим вариантом формулировки теоремы 3.5 является

Следствие 3.1. Два состояния автомата с n состояниями эквивалентны, если они (n — 1)-эквивалентны, и различимы, если они (n—1)-различимы.

Определение Р₁. Р₁ может быть определено с помощью следующего правила: состояния являются смежными в Р₁ тогда и только тогда, когда они для каждого входного символа дают одинаковые выходные символы. Определение Р_{k + 1} по P _k (k ≥ 1). Пары смежных состояний в Р _k, которые при любом входном символе переходят в смежные состояния в Р _k, представляют собой k-эквивалентные состояния, первые преемники которых по отношению к любому входному символу являются k-эквивалентными. Поэтому такие смежные состояния являются (k+1)-эквивалентными и должны быть смежными в Р _{k + 1}. Пары смежных состояний в Р _k, которые при некотором входном символе переходят в разобщенные состояния в Р _k, представляют собой k-эквивалентные состояния, первые преемники которых по отношению к некоторому входному символу являются k-различимыми. Поэтому такие смежные состояния являются (k + 1)-различимыми и должны быть разобщенными в P _{k + 1}. Два разобщенных состояния в Р _k должны быть разобщенными также в Р _k+1. Таким образом, Р _{k + 1} может быть определено по Р _k делением состояний каждого класса Р _k на подклассы таким образом, чтобы два состояния находились в одном и том же подклассе тогда и только тогда, когда их первые преемники по отношению к каждому входному символу являются смежными состояниями в Р _k. Полученные подклассы являются классами P _{k + 1}. Поскольку одноэлементные классы не могут быть разделены на подклассы, то такие классы Р _k могут быть автоматически включены в Р _{k + 1}.

Рассмотрим, например, разбиение Р₃ Для автомата A7, приведенное в (3.2). Первые преемники состояний 1, 3 и 8 являются смежными в Σ₃₂ при подаче α или β и в Σ₃₁ при подаче γ. Первые преемники состояний 5 и 7 являются смежными в Σ₃₃, если приложен входной символ а, в Σ₃₂, если приложен символ р, и в Σ₃₁, если приложен символ γ. Следовательно, {1, 3, 8} и {5, 6} являются классами Р₄. Первые преемники состояний 2 и 4 по отношению к каждому входному символу являются смежными состояниями в Р₃; поэтому {2, 4} являются классом Р₄. Одноэлементные классы {6} и {9} переходят в Р₄ без изменений. Полученное разбиение Р₄ будет таким, как показано в (3.3).

Таким образом, мы описали правила для последовательного построения Р _k для k=l, 2, 3,... Если для каждого входного символа каждая пара смежных состояний Р _k переходит в смежные состояния Р _k, то никакое дальнейшее разбиение Р _k невозможно и, следовательно, Р _k = 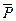. Описанные правила поэтому дают способ определения эквивалентного разбиения заданного автомата.

8.6. Разбиение при помощи таблиц Р_k

За исключением простейших случаев, процесс определения эквивалентного разбиения заданного автомата путем исследования таблиц переходов, графов или матриц, по существу, невозможен.

В этом параграфе мы опишем метод, по которому разбиение может быть выполнено систематически путем построения серий так называемых таблиц Р _k.

Таблица P _k заданного автомата, по существу, представляет собой то же, что и подтаблица s _v+1 для этого автомата со следующими отличиями: (1) Если {σi ₁, σi ₂,..., σi _r } представляют собой класс Р _k, то строки σi ₁, σi ₂,..., σi _r группируются вместе, при этом каждая группа строк отделяется линией от соседних групп. Порядок групп в таблице и порядок строк в каждой группе произвольны. Строки, принадлежащие к одной и той же группе и, следовательно, представляющие класс k-эквивалентности, будем называть смежными строками; строки, принадлежащие к различным группам, будем называть разобщенными строками. (2) Добавляется столбец 2, в котором указывается обозначение групп в таблице P _k. Обозначение групп произвольно и может выбираться независимо в каждой новой таблице P _k. (3) Каждое значение s _v+1 снабжается индексом, указывающим группу, к которой данное значение относится. Так, если строка σ _i; находится в группе, обозначенной «a», то каждое значение σ _i в подтаблице s _v+1 снабжается индексом «а».

Таблицы 3.3—3.6 являются таблицами Р₁, Р₂, Р₃ и Р₄ для автомата A7, изображенного на рис. 3.3.

Построение таблицы P₁ Изменим порядок строк в таблице переходов таким образом, чтобы одинаковые строки в подтаблице zv стали соседними. Каждая группа таких строк соответствует классу 1-эквивалентности, и, следовательно, является группой смежных строк в таблице Р1. Теперь можно построить таблицу Р₁ путем вычеркивания подтаблицы z _v, разделения групп строк линиями, добавления столбца 2 и снабжения индексами значений s _v+1, как было описано выше. В качестве иллюстрации сошлемся на таблицы 3.2 и 3.3.

Построение таблицы Р _k+1 по таблице P _k (k≥1). Две смежные строки в таблице Р _k, имеющие во всех столбцах

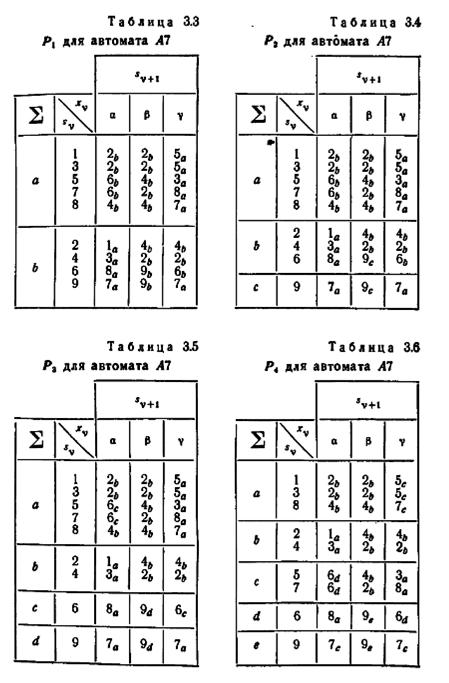
одинаковые индексы, являются смежными в таблице Р _k+1. Две смежные строки в таблице Р _k, имеющие в некоторых столбцах различные индексы, являются разобщенными в таблице Р _{k + 1}. Разобщенные строки в таблице Р _k являются также разобщенными в таблице Р _{k + 1}. Группа, состоящая из одной строки в таблице P _k, состоит из одной строки и в таблице Р _k+1. Таким образом, группы таблицы Р _{k + 1} могут быть выявлены проверкой индексов в таблице Р _k. После того как группы установлены, сама таблица может быть построена по описанному выше образцу. Приведенные здесь правила прямо вытекают из способа приписывания индексов и из описанных в § 3.5 условий определения P _{k + 1} по Р _k.

В качестве примера рассмотрим таблицу Р₃ автомата А7, представленную таблицей 3.5. В группе «а» одинаковые индексы во всех столбцах имеют строки 1, 3 и 8 и строки 5

и 7. (Индексы в строках 5 и 7 отличаются от индексов в строках 1,3 и 8.) Следовательно, строки 1, 3 и 8 и строки 5 и 7 образуют две группы строк в таблице Р₄. В группе «b» все строки имеют одинаковые индексы во всех столбцах, поэтому группа без изменений остается в таблице Р₄. Группы «с» и «d», содержащие по одной строке, могут быть перенесены без изменения в таблицу Р₄.

Если известны способы построения таблицы Р₁, а также таблицы P _{k + 1} по таблице P _k (k ≥ 1), то можно строить таблицы Р _k для последовательных значений k до тех пор, пока не будет получена таблица, в которой все смежные строки имеют одинаковые индексы во всех столбцах. В основном столбце в этих смежных строках обозначены эквивалентные состояния, а следовательно, группы последних представляют собой искомые классы эквивалентности. Согласно теореме 3.5, это условие должно иметь место для некоторого значения k ≤ n — 1. Для автомата А7 этому условию удовлетворяет таблица Р₄ (таблица 3.6).

Эквивалентное разбиение для А7 поэтому будет

Р: {1. 3, 8}, {2, 4}, {5, 7}, {6}. {9}. (3.9)