K-эквивалентность

Для дальнейших обсуждений полезно ввести понятие «k -эквивалентности».

Определение 3.2. Состояние σ _i автомата М₁ и состояние σ _j, автомата М₂ называются k-эквивалентными, если при приложении к М|σ _i и к M|σ _j входной последовательности длины k они вырабатывают одинаковые выходные последовательности. Если σ _i и σ _j не являются k-эквивалентными, то они называются k-различимыми. Обозначения М₁ и М₂ могут относиться к одному и тому же автомату.

Таким образом, σ _i и σ _j являются k-эквивалентными тогда и только тогда, когда, прикладывая входные последовательности длины k и наблюдая сигналы на внешних выходах, невозможно отличить автомат М₁ в состоянии σ _i от автомата М₂ в состоянии σ _j. Состояния σ _i и σ _j являются k-различимыми тогда и только тогда, когда имеется хотя бы одна входная последовательность длины k, которая при приложении к М₁| σ _i и М₂| σ _j, вырабатывает разные выходные последовательности. Два k-различимых состояния, согласно определению, данному в § 3.2, являются явно различимыми. На основании определения 3.2 легко показать, что k-эквивалентные состояния обладают свойствами рефлексивности, симметричности и транзитивности. Следовательно, k-эквивалентность можно трактовать как обычное отношение эквивалентности, которое непосредственно применимо к множествам состояний любой мощности. С другой стороны, k-различимость не обладает свойствами рефлексивности и транзитивности, и, следовательно, это понятие применимо только к парам состояний.

Лемма 3.4. (а) Если два состояния являются k-эквивалентными, то они являются и i-эквивалентными для каждого i≤k. (б) Если два состояния являются k-различимыми, то они являются и l -различимыми для каждого l≥ k.

Доказательство, (а) Пусть σ _i и σ _j являются k-эквивалентными, но различимыми при некоторой входной последовательности, скажем ε _i, длины l≤k. Тогда σ _i и σ _j должны быть различимы при входной последовательности ε _i ε _k-i, где ε _k-i представляет собой любую входную последовательность длины k - l. Следовательно, σ _i и σ _j являются k-различимыми, что противоречит условию, (б) Пусть σ _i и σ _j выявляются k-различимыми, но l - эквивалентными для некоторого l - k. Однако, согласно (а), если σ _i и σ _j являются l - эквивалентными, они должны быть k -эквивалентными для каждого k≤ l. Полученное противоречие доказывает справедливость утверждения (б).

Состояние, в которое переходит состояние σ _i, при подаче входной последовательности длины k называется k-м преемником σ _i, по отношению к этой последовательности. Нулевым преемником состояния является само состояние.

Теорема 3.2. Если состояния σ _i и σ _j являются k-эквивалентными и если их k-e преемники по отношению к любой входной последовательности длины k являются эквивалентными, то σ _i = σ _j.

Доказательство. Если σ _i и σ _j являются k-эквивалентными, то, согласно лемме 3.4, они вырабатывают одинаковые реакции при всех входных последовательностях длины k или менее. Если их k-e преемники по отношению к любой входной последовательности длины k являются эквивалентными, то они вырабатывают одинаковые реакции при всех входных последовательностях, которые следуют за первыми k символами. Следовательно, σ _i и σ _j вырабатывают одинаковые выходы при входных последовательностях любой длины, откуда следует, что σ _i = σ _j.

Теорема 3.3. Если состояния σ _i и σ _j являются эквивалентными, то их k-e преемники по отношению к любой входной последовательности длины k и для любого k являются эквивалентными.

Доказательство. Пусть σ´ _i и σ´ _j, являются k-ми преемниками состояний σ _i и σ _j соответственно по отношению к произвольной входной последовательности ε _k. Если σ´ _i ≠σ´ _j, то имеется последовательность, скажем ε _i для которой σ´ _i и σ´ _j, вырабатывают различные реакции. Следовательно, реакции для σ _i и σ _j на ε _k ε _i должны быть разными; это противоречит допущению, что σ _i = σ _j.

Входную последовательность, подаваемую на М₁| σ _i и М₂| σ _j, можно сравнить с двумя путями, начинающимися состояниями σ _i и σ _j на графе переходов для автоматов М₁ и М₂ соответственно. Теорема 3.3 означает, что если два

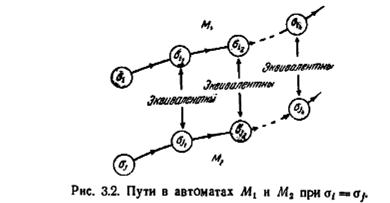
начальных состояния на этих путях эквивалентны, то каждые два соответствующих состояния на этих путях (т. е. состояния, в которые переходят автоматы из начальных состояний после прохождения одного и того же числа дуг) являются также эквивалентными. Это положение иллюстрируется рис. 3.2, где показанные пути являются путями, которые проходят M₁ и М₂, при приложении некоторой входной последовательности к М₁| σ _i и к М₂| σ _j. Если σ _i и σ _j являются эквивалентными, то k-e преемники σ i_k и σ j_k должны быть эквивалентны для всех k.

Изложенные результаты могут быть использованы во многих случаях для установления эквивалентности состояний, когда эквивалентность других состояний уже установлена. Пусть, например, известно, что пары состояний {1, 5} и {3, 7} автомата Л6, изображенного на рис. 3.1, являются эквивалентными. Тогда пара {4, 8} должна быть также парой эквивалентных состояний вследствие того, что 4 и 8 являются 1-эквивалентными, а их первыми преемниками являются пары {1,5} и {3, 7}. Если известно, что состояния в паре {4, 8} эквивалентны, то состояния в парах {1,5}, {2, 6} и {3, 7} должны быть также эквивалентными, поскольку они образуют пары соответствующих состояний на путях, начинающихся состояниями 4 и 8.