Метод разбиения, описываемый в настоящем параграфе, по существу, такой же, как метод, описанный в § 3.6; разница состоит в том, что операции производятся над матрицей переходов, а не над подтаблицей s v+1. Хотя метод матричного разбиения не имеет преимуществ по сравнению с методами, описанными выше, он дает новую и полезную интерпретацию понятия классов эквивалентности.
Симметрической перестановкой относительно матрицы называется перестановка строк и столбцов матрицы по одному и тому же правилу. Следовательно, если обозначения, присвоенные строкам и столбцам матрицы [М], симметричны относительно главной диагонали, то эти обозначения будут симметричными в любой симметрической перестановке этой матрицы. Симметрическое разбиение [М] представляет собой разделение групп строк и столбцов пунктирными линиями таким образом, что если имеется пунктирная линия, разделяющая строки σ i и σ j, то имеется также пунктирная линия, разделяющая столбцы at и Oj, и наоборот. Матрица [M](k) для автомата М является матрицей [М], в которой. симметрическая перестановка и симметрическое разбиение обладают следующими свойствами: строки (и столбцы), соответствующие смежным состояниям P k, сгруппированы вместе, а каждая группа отделена от соседних групп пунктирными линиями; порядок групп в матрице и порядок строк (столбцов) в каждой группе произвольны; если Р k содержит r k классов, то симметрическое разбиение образует r k рядов подматриц с r k подматрицами в каждом ряду.
|
|
|
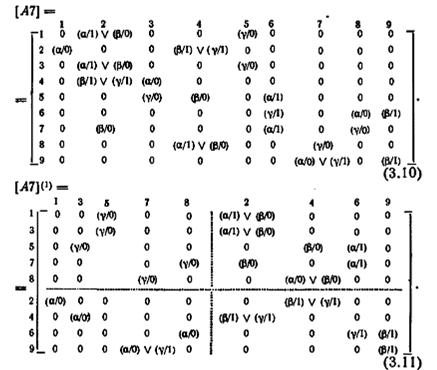
Построение матрицы М (1). Сгруппируем строки матрицы [М] так, чтобы две строки принадлежали к одной и той же группе тогда и только тогда, когда они образуют одинаковые множества пар вход-выход. Каждая такая группа представляет собой класс 1-эквивалентности. Производя симметрическую перестановку и симметрическое разбиение [М] в соответствии с правилами, описанными выше, получим [M](1). Примером матрицы переходов является матрица (3.10) автомата А7 (рис. 3.3). Строки 1, 3, 5, 7 и 8 в [А7] представляют пары вход-выход (α/1), (β/0) и (γ/О). Строки 2, 4, 6 и 9 представляют пары вход-выход (α/0), (β/1) и (γ/1). Тогда матрица [A7](1) строится группировкой строк (и столбцов) 1, 3, 5, 7 и 8 и строк (и столбцов) 2, 4, 6 и 9, при этом группы разделяются пунктирной линией. Матрицей [A7](1), полученной в результате этих операций, является матрица (3.11).
Построение матрицы [M](k+1) пo [M](k) (k≥1). Пусть σ i и σ j — две строки в одной и той же группе строк [M](k). Если в каждой из подматриц, пересеченных строками σ i и σ j, строки σ i и σ j имеют одинаковые множества пар вход-выход, то σ i и σ j представляют собой k-эквивалентные состояния, первые преемники которых по отношению к любому вход-входному символу являются k-эквивалентными, поэтому состояния σ i и σ j являются (k+1)-эквивалентными. Если эти условия не имеют места, то σ i и σ j являются (k + 1)-различимыми. Таким образом, матрица [M](k+1) может быть построена по [M](k), если разделить каждую группу строк в [M](k) на подгруппы так, чтобы две строки принадлежали одной и той же подгруппе тогда и только тогда, когда они имеют одинаковые пары вход-выход в каждой из пересекаемых ими подматриц r k. Каждая такая группа представляет собой (k + 1)-эквивалентный класс. Произведя симметрическую перестановку и симметрическое разбиение матрицы [M](k), получим в результате [M](k + 1). Например, строки 1, 3, 5, 7 и 8 в [A7](1) имеют одинаковые множества пар вход-выход в каждой подматрице, которую они пересекают. С другой стороны, строки 2, 4 и 6 образуют в пересекаемых подматрицах множества пар вход-выход, которые отличаются от множества пар вход-выход, образованного строкой 9. Следовательно, строки 2, 4 и 6 и строка 9 дают две различные группы в [A7](1), как показано в (3.12).
|
|
|
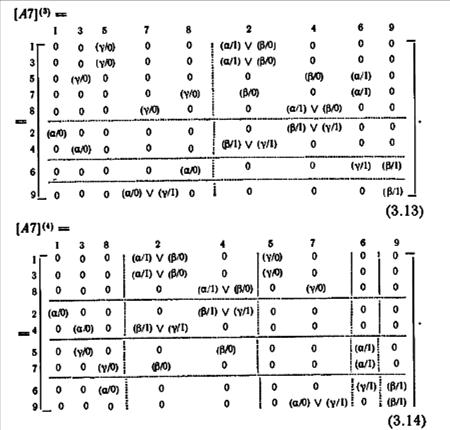
Матрица [M](k) дает эквивалентное разбиение тогда, когда никакое дальнейшее разбиение не может быть произведено (т. е. когда каждая подматрица имеет одну строку и один столбец или когда строки внутри каждой подматрицы имеют одинаковые множества пар вход-выход). При этих условиях различные группы строк (или столбцов) являются классами k-эквивалентности, где k может быть сделано сколь угодно большим; поэтому эти группы представляют собой классы эквивалентности автомата М. Согласно теореме 3.5, это может иметь место для некоторого значения k≤n— 1.
Матрицы (3.10)—(3.14) иллюстрируют описываемый метод эквивалентного разбиения автомата А7. Матрица [A7](4) дальнейшее разбиение которой невозможно, очевидно, содержит эквивалентное разбиение {1, 3, 8}, {2, 4}, {5, 7}, {6} и {9}, совпадающее с разбиением (3.9).

 2015-02-27
2015-02-27 1175
1175
