Эквивалентность автоматов

Понятие эквивалентности можно распространить на весь автомат с помощью следующих определений:

Определение 3.3. Говорят, что автомат М ₁ и автомат М ₂ эквивалентны, если каждому состоянию σ _i автомата М₁ соответствует, по крайней мере, одно эквивалентное ему состояние в автомате М₂ и если каждому состоянию σ _j автомата М₂ соответствует, по крайней мере, одно эквивалентное ему состояние в автомате M₁. Если автоматы М₁ и М₂ не эквивалентны, то они различимы. Таким образом, М₁ и М₂ являются эквивалентными тогда и только тогда, когда, наблюдая сигналы на их выходах, нельзя отличить автомат М₁ в любом из его состояний от автомата М₂ и автомат М₂ в любом из его состояний от автомата М₁.

Автоматы М₁ и М₂ являются различимыми тогда и только тогда, когда имеется, по крайней мере, одно состояние в М₁, которое не является эквивалентным никакому состоянию в М₂ или если имеется, по крайней мере, одно состояние в М₂, которое не является эквивалентным никакому состоянию в М₁.

Эквивалентность автоматов М₁ и М₂ обозначается равенством М₁ = М₂, а различимость автоматов М₁ и М₂ — неравенством М₁ ≠ М₂. Пользуясь определением 3,3 легко показать, что эквивалентность автоматов обладает свойством рефлексивности (M_i = M _i), свойством симметричности (если M _i = M _j, то M _j = M _i) и свойством транзитивности (если M _i = M _j и M _j = M _k, то M _i = M _k). Следовательно, эквивалентность автоматов может рассматриваться как обычное отношение эквивалентности и применяться непосредственно к множествам автоматов любой мощности. С другой стороны, различимость автоматов не обладает свойствами рефлексивности и транзитивности и поэтому может относиться только к паре автоматов.

Определение эквивалентности автоматов означает, что два автомата, имеющих одинаковые таблицы переходов (или графы или матрицы), должны быть эквивалентны. Кроме того, поскольку эквивалентность или различимость пары состояний не зависит от обозначений состояний, то два изоморфных автомата также должны быть эквивалентными.

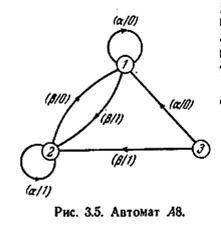
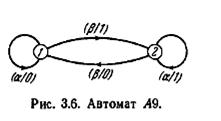
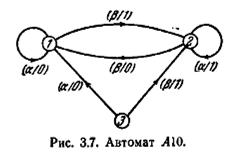
Автоматы A8 и A9, изображенные на рис. 3.5 и 3.6 соответственно, представляют собой два эквивалентных автомата. В этом можно убедиться, если обратить внимание на то, что A9 становится автоматом A8, если не учитывать состояние 3 автомата A8. Следовательно, состояния 1 и 2 автомата A8 эквивалентны соответственно состояниям 1 и 2 автомата A9. Кроме того, состояния 1 и 3 автомата A8 явно эквивалентны и, следовательно, эквивалентны; поэтому состояние 3 A8 эквивалентно стоянию 1 A9. Таким образом, для каждого состояния A8 мы находим эквивалентное состояние A9 и для каждого состояния A9 находим эквивалентное состояние A9. Это означает, что A8 и A9 являются эквивалентными автоматами. Сравнивая автомат A9 с автоматом A10, изображенным на рис. 3.7, можно заметить, что A9 становится одинаковым с A10, если не учитывать состояние 3 А10; следовательно, для каждого состояния A9 мы находим эквивалентное состояние A10. Однако, поскольку пары состояний {1, 3} и {2, 3} являются явно различимыми и, следовательно, различимыми, утверждение, обратное последнему, не верно. Поэтому A9 и A10 не являются эквивалентными.