Пусть М — автомат с ṅ эквивалентными классами, обозначенными Σ1, Σ2,..., Σṅ, и пусть σ i представляет собой какое-нибудь состояние в Σi. Минимальная форма автомата М, обозначаемая через М, представляет собой автомат с ṅ состояниями, образующими множество {σ´1, σ´2,..., σ´ṅ}. Минимальный автомат строится из М следующим образом. Обозначим характеристические функции автомата М через f z и f s, а автомата Ṁ через f z и f s; тогда, если
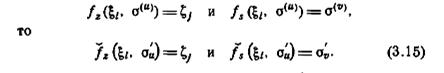
Заметим, что если при приложении ξ i к М в определенном состоянии из Σu вырабатывается выходной символ ζ j, то при приложении ξ i в любом состоянии из Σu также вырабатывается выходной символ ζ j. Аналогично, если при приложении ξ i к М в некотором состоянии из Σu М переходит в состояние, принадлежащее Σ v, то при приложении ξ i в любом состоянии из Σu М переходит в состояние, принадлежащее Σ v. Таким образом, при построении Ṁ по условию (3.15) не возникает никакой неопределенности вследствие того, что σ(u) является произвольным состоянием, принадлежащим классу Σu, и что σ( v ) является произвольным состоянием, принадлежащим классу Σ v.
Процесс отыскания минимальной формы автомата называется минимизацией автомата. Минимизация автомата М состоит в определении эквивалентного разбиения Жив последующем применении (3.15) для построения Ṁ. Так как при применении (3.15) все состояния М, принадлежащие одному и тому же классу эквивалентности, дают один и тот же результат, то индивидуальное распознавание каждого состояния становится ненужным; для целей минимизации важно распознавание класса, к которому принадлежит каждое состояние. Поэтому всем состояниям М, принадлежащим классу эквивалентности Σ i, можно приписать общее обозначение, например, σ´ i После этого (3.15) может быть интерпретировано как формулировка того, что автомат Ṁ получается из автомата М путем «объединения» одинаково обозначенных состояний в одно состояние. Способы, которыми это объединение производится, существенно зависят от того, каким образом определен автомат — таблицей, графом или матрицей. Эти способы будут описаны ниже. Хотя понимание этих способов облегчается благодаря предшествующей интуитивной интерпретации условия (3.15), их справедливость не зависит от этой интерпретации и вытекает непосредственно из самого условия.
Таблица переходов Ṁ. Если заданы таблица переходов и эквивалентное разбиение Σ1, Σ2,..., Σṅ, автомата М, то таблица переходов автомата М может быть построена следующим образом: (1) заменим обозначение каждого состояния, которое имеется в таблице переходов М, на обозначение класса, которому данное состояние принадлежит; (2) из каждой группы строк с одинаковыми обозначениями в клетках основного столбца (все такие строки являются одинаковыми в обеих подтаблицах z v и s v+1) вычеркнем все строки, кроме одной. Полученная при этом таблица является таблицей переходов М.
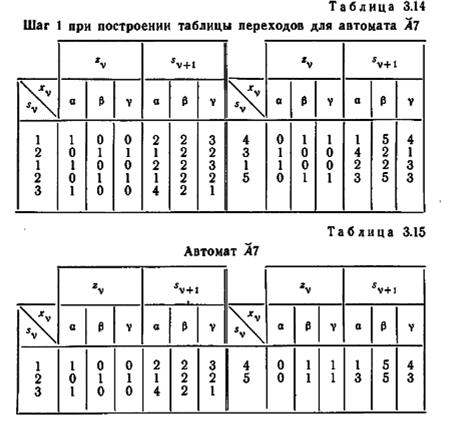
Например, автомат А7, представленный таблицей 3.2, имеет классы эквивалентности {1, 3, 8}, {2, 4}, {5, 7}, {6} и {9}. Обозначим их произвольно 1, 2, 3, 4 и 5 соответственно. Делая первый шаг процедуры, заменим каждое обозначение «1», «3», и «8» в основном столбце и в s v+1 подтаблице таблицы 3.2 на «1», каждое «2» и «4»—на «2», «5» и «7» — на «3», «6» — на «4», «9» — на «5». Полученная в результате таблица переходов приведена в таблице 3.14. Вычеркивание всех повторяющихся строк дает таблицу переходов А7, показанную в таблице 3.15-
Граф переходов Ṁ. Если заданы граф переходов и эквивалентное разбиение Σ1, Σ2,..., Σṅ автомата M, то граф переходов автомата Ṁ может быть построен следующим образом: (1) заменим обозначение каждого состояния, которое имеется в графе переходов М, на обозначение класса, к которому относится данное состояние; (2) объединим все одинаково обозначенные состояния (рассматривая дуги графа как «гибкие связи») и представим объединенные состояния одним состоянием, имеющим общее обозначение; (3) из каждой группы дуг, имеющих общее исходное состояние и общее конечное состояние (все такие дуги обозначены одинаково), вычеркнем все, кроме одной. Полученный в результате граф будет графом Ṁ.
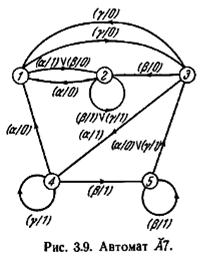
В качестве примера на рис. 3.9 приведен граф переходов автомата А7, полученный в результате применения описанной выше процедуры к графу переходов, изображенному на рис. 3.3. Использованные здесь обозначения классов эквивалентности А7 те же, что были использованы при построении таблицы переходов.
Матрица переходов Ṁ. Если заданы матрица переходов и классы эквивалентности Σ1, Σ2,..., Σṅ автомата М, то матрица переходов автомата М может быть построена следующим образом: (1) произведем симметрическую перестановку и симметрическое разбиение [М], так чтобы строки (и столбцы) группировались соответственно классам эквивалентности М (в результате получим матрицу такую же, как окончательная матрица [M]( k ), получаемая при матричном методе эквивалентного разбиения); (2) заменим все обозначения строк (и столбцов) каждой группы, представляющей класс эквивалентности, одним обозначением этого класса; (3) заменим каждую подматрицу в разбитой матрице одной клеткой, содержащей все пары вход-выход, которые имеются в любой строке этой подматрицы (все строки в любой такой подматрице содержат одно и то же множество пар вход-выход). Полученная в результате матрица будет матрицей переходов Ṁ.
В качестве примера приведена матрица (3.16), представляющая собой матрицу переходов А7(с волной), построенную по показанной в (3.14) матрице [A7](4). Использованные здесь обозначения классов эквивалентности А7 те же, что при
построении таблицы переходов

 2015-02-27
2015-02-27 510
510







