Класс минимальных автоматов

Используя определения, введенные в § 2.3, в качестве следствия теоремы 3.1 и определения эквивалентности автоматов получаем:

Лемма 3.12. Явно минимальный (n, р, q)-автомат должен быть минимальным. Явно сократимый (n, р, q)- автомат не может быть минимальным.

Дополнительно теперь докажем следующие леммы.

Лемма 3.13. Мощность семейства перестановок минимального (n, р, q)-автомата равна n!

Доказательство. Пусть М₁— минимальный (n, р, q)- автомат и пусть М₂ — автомат, полученный из М₁ перестановкой обозначений его состояний. Предположим, что перестановка, с помощью которой М₂ получен из М₁, включает в себя замену обозначения состояния σ _i из М₁ на «σ _j» (j ≠ i). Если М₁ и М₂ имеют одинаковые таблицы переходов, то реакции M₁|σ _j и М₂| σ _i на любую входную последовательность должны быть одинаковыми и, следовательно, реакции M₁|σ _j и M₂|σ _j на любую входную последовательность также должны быть одинаковыми. Это означает, что состояния σ _i и σ _j в М₁ эквивалентны и, следовательно, М₁ не является минимальным автоматом. Из полученного противоречия следует, что различные перестановки должны давать в результате различные таблицы переходов. Число различных перестановок равно n!. Лемма доказана.

Лемма 3.14. Мощность Ň_n,p,q класса минимальных (n, р, q)-автоматов, таких, среди которых нет двух изоморфных друг другу автоматов, определяется выражением

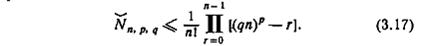
Доказательство. Пусть число (n, р, q)-автоматов, не являющихся явно сократимыми, равно Ňⁿ_n,p,q и пусть число минимальных (n, р, q) -автоматов, изоморфных или неизоморфных друг другу, равно Ň´_n,p,q. Тогда, согласно лемме 3.12,

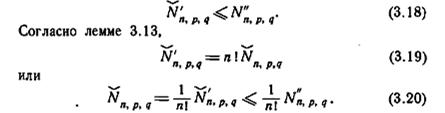
Используя уравнение (2.3) для определения Ň´´_n,p,q, получаем доказательство леммы. Поскольку два минимальных неизоморфных автомата должны быть различимы, то Ň_n,p,q представляет собой также число минимальных (n, р, q)-автоматов, среди которых нет ни одной пары эквивалентных автоматов. Это число должно включать в себя число Ň^(ям)_n,p,q явно минимальных (n, р, q)- автоматов, среди которых нет ни одной пары изоморфных автоматов. Используя теорему 2.1 для определения Ň^(ям)_n,p,q получаем:

Теорема 3.7. Мощность Ň_n,p,q класса минимальных (n, р, q)-автоматов, среди которых нет ни одной пары эквивалентных автоматов, определяется выражением

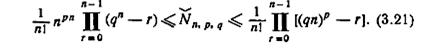
Например, общее число минимальных (2,2,2)-автоматов, среди которых нет эквивалентных, заключено между 96 и 120.

Задачи

3.1. Покажите, что если σ _i = σ _j, a σ _j ≠ σ _k, то σ _i ≠ σ _k,.

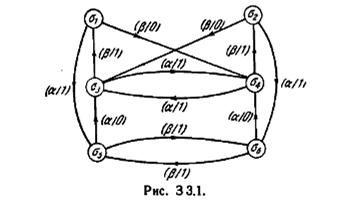
3.2. Используя симметричность графа переходов, показанного на рис. 3 3.1, покажите, что σ ₁ = σ ₂, σ ₃ = σ ₄ и σ ₅ = σ ₆.

3.3. В подтаблице z _v автомата М все строки одинаковы. Покажите, что М представляет собой тривиальный автомат.

3.4. Покажите, что если iя и j-я строки матрицы [М] одинаковы, то состояния σ _i и σ _j автомата М являются эквивалентными.

3.5. Состояния σ _i и σ _j являются k₁-эквивалентными, а их k₁-e преемники по отношению к любой входной последовательности длины k₁ являются k₂-эквивалентными. Покажите, что если k₁ + k₂ ≥ n-1, то σ _i = σ _j.

3.6. Состояния σ _i и σ _j являются k₁-эквивалентными, а их k₁-e преемники по отношению к любой входной последовательности длины k₁ являются k₂-эквивалентными, но (k₂ + 1)-различимыми. Покажите, что если σ _i ≠ σ _j, то k₁ + k₂ ≤ n+2.

3.7. Автомат М имеет 1-эквивалентные классы Σ1₁, Σ1₂,..., Σ1_i

где Σ1_i, i=1, 2,.... r, содержит n_i состояний. Сосчитайте число строк в таблице пар для М.

3.8. Разбиение Р₁ автомата с n состояниями имеет r классов. (а) Если Р_k ≠ Р _k-1 каково минимальное число классов в Р _k. (б) Если Р_k ≠ Р _k-1 каково максимальное число состояний в одном классе Р _k? (в) Каково наименьшее значение k, при котором Р _k является заведомо одинаковым с P _k+i?

3.9. Таблица 3 3.1 представляет собой частично заполненную Р₃ таблицу автомата с шестью состояниями. Определите 2-эквивалентное разбиение этого автомата.

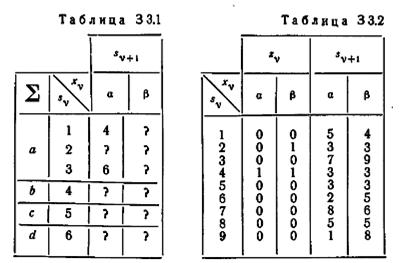
3.10. Найдите эквивалентное разбиение автомата, определенного таблицей 3 3.2: (а) построением P _k таблиц, (б) методом таблицы пар.

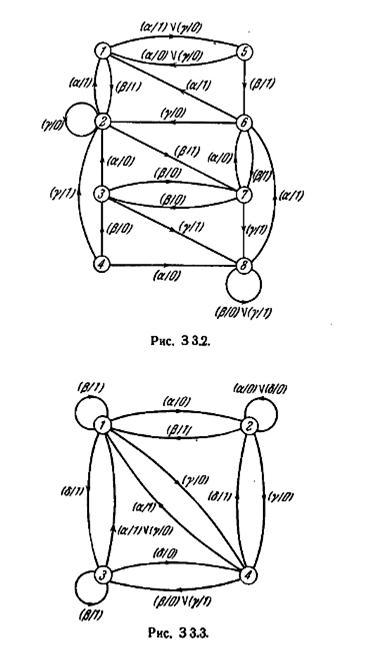
3.11. Определите эквивалентное разбиение автомата, определенного графом на рис. 3 3.2: (а) построением Р _k таблиц, (б) методом таблицы пар, (в) катричным разбиением.

3.12. Покажите, что если М₁ = М₂ и М₂ ≠ М₃, то М₁ ≠ М₃.

3.13. Рис. 3 3.3 представляет собой граф переходов автомата с четырьмя состояниями. Постройте граф переходов автомата с пятью состояниями, эквивалентный заданному на рис. 3 3.3.

3.14. Каждое состояние автомата М₁ эквивалентно некоторому состоянию автомата М₂, но М₁ ≠ М₂. Покажите, что автомат M₁ эквивалентен либо изолированному, либо тупиковому подавтомату М₂.

3.15. Пусть состояние σ _i автомата М₁ эквивалентно состоянию σ _j автомата М₂. Известно, что имеется некоторая входная последовательность, которая проводит М₁|σ _i через все состояния M₂ и в то же время проводит М₂|σ _j через все состояния М₂. Покажите, что М₁ = М₂.

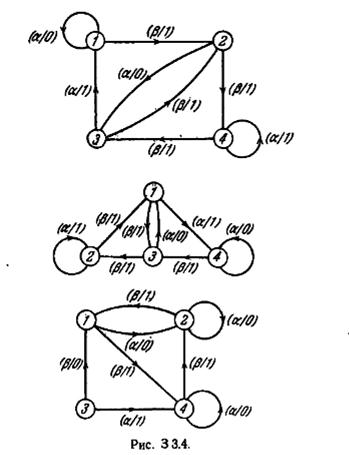
3.16. Определите, какие два из трех автоматов, показанных на рис. 3 3.4, являются эквивалентными и какие различимыми. Который из автоматов является минимальным?

3.17. Покажите, что если автомат М´ является тупиковым или изолированным подавтоматом автомата М, то Ṁ содержит подавтомат М´´, который является минимальной формой М´, либо тупиковым подавтоматом Ṁ, либо изолированным подавтоматом Ṁ, либо, наконец, автоматом Ṁ.

3.18. Покажите, что если М₁ = М₂ =... = M _N, то Ṁ₁ представляет собой минимальную форму автомата ∆(М₁, М₂,..., М _N).

3.19. Покажите на примере, что два неминимальных эквивалентных автомата, имеющих одинаковое число состояний, не обязательно являются изоморфными.

3.20. Дано два автомата (не обязательно минимальных); сформулируйте алгоритм для определения, являются они изоморфными или нет.

3.21. Определите минимальные формы автоматов, заданных в задачах 1.2—1.9 главы 1.

3.22. Постройте таблицу, граф и матрицу переходов минимальной формы автомата, показанного на рис. 3 3.2.

3.23. Сформулируйте правило определения всех явно эквивалентных пар состояний по таблице пар.

3.24. Получите минимальную форму автомата, изображенного на рис. 3 3.2, методом последовательного объединения, описанным в § 3.13.