Свойства минимальной формы

В дальнейшем будем говорить, что автомат М₁ меньше или больше М₂ в зависимости от того, имеет М₁ соответственно меньшее или большее число состояний по сравнению с М₂.

Теорема 3.6. Если Ṁ является минимальной формой автомата М, то: (а) Ṁ является единственной минимальной формой с точностью до изоморфизма[20]; (б) Ṁ=М; (в) никакие два состояния в Ṁ не являются эквивалентными; (г) не существует автомата, эквивалентного М и меньшего, чем Ṁ.

Доказательство, (а) По лемме 3.5 P _k является единственным для любого k≥1 и, следовательно, P _n-1 = Ṗ является единственным. Так как при определенном Ṗ построение Ṁ из M является единственным, не учитывая обозначения, то Ṁ является единственным с точностью до изоморфизма, (б) Рассмотрим какую-нибудь входную последовательность ξi₁, ξi₂,..., ξi_i, приложенную к M|σ^(u). Пусть соответствующая последовательность состояний будет σ^(u1), σ^(u2),..., σ^(ui),и соответствующая выходная последовательность будет ζj₁, ζj₂,..., ζj _i. Теперь пусть та же входная последовательность приложена к Ṁ|σ´ _u. По условию (3.15), на основании которого строится Ṁ по М, соответствующая последовательность состояний должна быть σ´_u1, σ´_u2,..., σ´_ui и соответствующая выходная последовательность должна быть ζj₁, ζj₂,..., ζj _i. Поскольку в приведенных рассуждениях i и u являются произвольными, то, следовательно, любое состояние М, принадлежащее классу эквивалентности Σ_u, является эквивалентным состоянию σ´ _u автомата Ṁ. Таким образом, для каждого состояния М мы находим эквивалентное состояние Ṁ и для каждого состояния Ṁ находим эквивалентное состояние М, что означает, что Ṁ= М. (в) Пусть σ´ _u и σ´ _v являются двумя любыми состояниями Ṁ (u ≠ v).

Из доказательства части (б) следует, что σ _u эквивалентно состояниям М, принадлежащим классу эквивалентности Σ_u, а σ´ _v эквивалентно состояниям М, принадлежащим классу эквивалентности Σ _v. Так как ни одно состояние- из класса Σ_u не эквивалентно никакому состоянию из класса Σ _v, то состояния σ´ _u и σ´ _v автомата Ṁ должны быть различимыми, (г) Предположим, что имеется автомат М´, эквивалентный М и меньший Ṁ. Так как Ṁ = M и М´=М, то это значит, что М´ = Ṁ и что каждое состояние Ṁ является эквивалентным некоторому состоянию М´. Так как Ṁ больше, чем М´, то имеются, по крайней мере, два состояния Ṁ, которые эквивалентны одному и тому же состоянию М´ и, следовательно, эквивалентны друг другу. Однако, согласно части (в) теоремы, это невозможно, что доказывает от противного тот факт, что не существует автомата, эквивалентного М, и меньшего, чем Ṁ.

Автомат, который является своей минимальной формой и потому не имеет эквивалентного себе меньшего автомата, называется минимальным автоматом. Автомат, имеющий n состояний и n классов эквивалентности, в котором, следовательно, все пары состояний различимы, является минимальным автоматом. Из теоремы 3.6 следует, что если задан какой-либо автомат М, то мы можем найти минимальный автомат Ṁ, эквивалентный М и являющийся единственным с точностью до изоморфизма. Этот вывод является исключительно важным, поскольку он говорит нам, что каждый автомат имеет некоторое «каноническое» представление, независящее от способа задания исходного автомата. Действительно в общем случав существует ряд способов, которыми автомат может быть описан (особенно если это сделано устно), и оказывается, что все это многообразие описаний может быть, в конце концов, сведено к некоторому стандартному представлению. Более того, из сделанного вывода следует, что стандартное представление является наиболее компактным в смысле числа используемых состояний. Если вследствие недостатка опыта или изобретательности у исследователя начальное представление получается сильно избыточным, то имеется прямой способ уменьшить избыточность до предела и получить минимальное представление.

Чтобы проиллюстрировать сказанное, рассмотрим следующую игру: монета подбрасывается многократно; очко засчитывается при v-м подбрасывании, если при (v—2)-м, (v—1)-м и v-м подбрасывании выпадают соответственно: цифра, герб, герб или герб, герб, герб; в других случаях очко не засчитывается. Обозначив «герб» буквой «Г», а «цифру»—буквой «Ц», «очко» — «1», а «отсутствие очка» — «О», мы можем выбрать следующие входной алфавит, выходной алфавит и множество состояний:

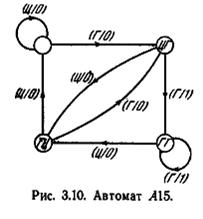
где указанные четыре состояния отождествляются со всеми возможными исходами при (v — 2)-м и (v—1)-м подбрасывании. Граф переходов автомата A15, соответствующего этому описанию игры, показан на рис. 3.10. Однако более компактное представление получается, если заметить, что счет очков при v-м подбрасывании не зависит на самом деле от (v — 2)-го исхода (хотя это может быть замаскировано устным описанием игры). Тогда мы можем выбрать следующие входной и выходной алфавиты и множество состояний:

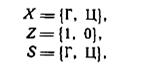
где указанные два состояния отождествляются со всеми возможными исходами при (v—1)-м подбрасывании. В результате получим граф переходов для автомата A16, изображенный на рис. 3.11.

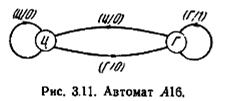
Методом, описанным в § 3.10, легко проверить, что A16 = A15. Таким образом, если мы не сумели обнаружить избыточности в устном описании, мы все равно можем получить A16 (с точностью до изоморфизма) применением к A15 любой стандартной методики минимизации автоматов.

Попутно заметим, что роль, которую играет минимальная форма в теории конечных автоматов, аналогична роли, которую играет «эквивалентная схема Тевенена» в теории линейных "цепей. Оба представления системы служат для описания ее поведения, наблюдаемого на доступных выводах, наиболее компактным способом.