Уменьшение числа состояний автомата последовательным объединением

Пусть М — автомат, о котором известно, что его состояния σ _i и σ _j эквивалентны. Объединением состояний σ _i и σ _j по правилам объединения эквивалентных состояний при минимизации, описанным в § 3.11, мы можем получить другой автомат М₁. При этом состояния σ _i и σ _j заменяются одним состоянием, скажем σ _ij, которое переходит в то же состояние, что и σ _i (или σ _j), и вырабатывает такой же выходной символ, как и σ _i (или σ _j), при приложении одного и того же входного символа. Это значит, что otj эквивалентно σ _i и σ _j и, следовательно, М₁ — М. Далее, если известно, что в М₁ имеются два эквивалентных состояния, то, повторяя описанную операцию объединения, можно получить М₂ = M₁ Эта процедура может повторяться до тех пор, пока не будет получен М _k = M _k-1 не имеющий эквивалентных состояний. Обозначая исходную форму автомата М через Мо, можно установить, что M _k (k≥1), полученный с помощью описанной процедуры, всегда меньше М _k-1 и, следовательно, представляет собой сокращенную форму М.

Сокращение автомата последовательным объединением особенно удобно, когда рассматриваемый автомат имеет явно эквивалентные состояния, которые могут быть отмечены при рассмотрении таблицы переходов. Поскольку, согласно теореме 3.1, явно эквивалентные состояния являются эквивалентными, то для сокращения заданного автомата они могут быть объединены, как описано в предыдущем абзаце. Объединение двух явно эквивалентных состояний, скажем σ _i и σ _j, наиболее удобно выполнять по таблице переходов, вычеркивая строку Oj и заменяя всюду в подтаблице s _v+1 обозначение «σ _i» и «σ _j».

В качестве примера приведены таблицы 3.16 — 3.19, в которых даны последовательные стадии сокращения автомата A6, изображенного на рис. 3.1 и в таблице 3.1. Для удобства таблица 3.1 воспроизведена здесь еще раз как таблица 3.16. В этой таблице пары состояний {1,5} и {2,6} являются явно эквивалентными; вычеркивая строки 5 и 6 и

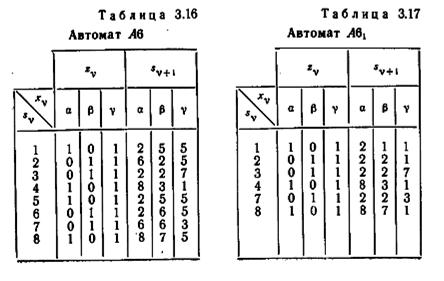
заменяя каждое из обозначений «5» на «1» и_каждое «6» на «2», получим автомат А6₁= А6, представленный таблицей 3.17.

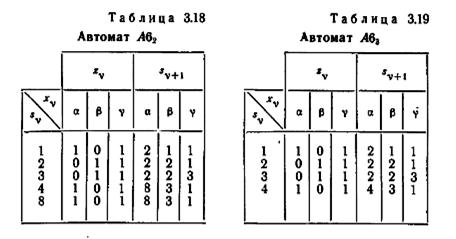
В А6₁ пара состояний {3,7} является явно эквивалентной; вычеркивая строку 7 и заменяя каждое обозначение «7» на «3»,

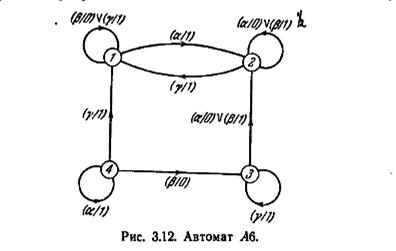
получаем автомат A6₂=A6₁, представленный таблицей 3.18. В A6₂ явно эквивалентной является пара {4,8}. Вычеркивая строку 8 и заменяя каждую цифру «8» на «4», получим автомат A6₃= A6₂, представленный таблицей 3.19. Поскольку в A6₃ нет явно эквивалентных состояний, сокращение путем объединения в том виде, в каком оно выполнялось выше, должно на этом закончиться. Оказывается, что полученный сокращенный автомат A6₃ является в то же время минимальной формой A6. Граф переходов A6₃=A6 показан на рис. 3.12.

Следует подчеркнуть, что, поскольку не всякие два эквивалентных состояния являются явно эквивалентными, описанная процедура сокращения не всегда дает минимальный автомат. После того как методом последовательного объединения получен наименьший автомат, следует применять стандартную методику эквивалентного разбиения, чтобы получить минимальную форму автомата или чтобы удостовериться в том, что дальнейшее сокращение невозможно.