Простые условные диагностические эксперименты

Рассмотрим в диагностическом дереве для М и А (М) путь, который ведет к A-группе G, содержащей простое σ-множество, например {σ´_i} (сама G не обязательно является простой, так как она может содержать другие непростые σ -множества). Если этот путь описывает входную последовательность ε, то А (М) должно содержать состояние, например σ´_i, преемником которого по отношению к ε является состояние σ´ _i. Так как множество {σ´_i} в G является одноэлементным, то реакция σ_i на ε, по лемме 4,2, не может быть приписана никакому состоянию из А(М), за исключением σ _i. Следовательно, если случайно σ _i является истинным начальным состоянием М, то его можно распознать входной последовательностью, которая не обязательно описывается диагностическим путем. Используя этот факт, можно применять минимальные диагностические последовательности по частям, а не целиком, в надежде, что начальное состояние таково, что его можно распознать с использованием лишь части всей последовательности. Эта схема составляет решение диагностической задачи для т состояний с помощью простого условного эксперимента.

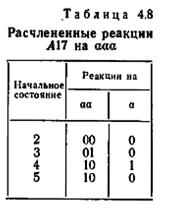
Деление минимальной диагностической последовательности на подпоследовательности выполняется следующим образом. Пусть ε_k есть k-я подпоследовательность и пусть G _k представляет собой A-группу, к которой ведет путь, описываемый ε₁ε_2... ε_k; обозначим А(М) через G₀. Тогда ε_k есть подпоследовательность, описываемая подпутем, который ведет от G _k-1 к первой A-группе, которая содержит, по крайней мере, одно более простое σ -множество, чем G _k-1. Так как решение G₀ равно 1 и так как число σ -множеств в A-группе не может превышать мощности т, соответствующей А(М), то число подпоследовательностей, полученных таким образом, не может превышать m — 1. Так, например, автомат A17 на рис. 4.3 и множество допустимых начальных состояний {2,3,4,5} дают G₀={2, 3, 4, 5}, G₁={1}, {2}, {5,1}, G₂={1}, {1}, {2}, {1}; следовательно, ε₁ = aa и ε₂ = a (см. рис. 4.7). После того как определены подпоследовательности, условный эксперимент может быть выполнен следующим образом.

Алгоритм 4.3. Даны автомат М, его множество допустимых начальных состояний A(M) = {σi₁, σi₂,..., σi_m} и разделенная на части диагностическая последовательность ε₁ε_2... ε_k; требуется распознать начальное состояние М с помощью простого условного эксперимента. (1) Составим перечень реакций М|σi₁, М|σi₂,..., М|σi_m на ε₁ε_2... ε_r В соответствии с разделением входной последовательности разделим каждую реакцию на r подпоследовательностей. Пусть k=1. (2) Приложим ε_k к М. (3) (а) Если реакция М на ε₁ε_2... ε_k является свойственной только одному состоянию в перечне, составленном в (1), то это состояние есть начальное состояние М. (б) Если реакция М на ε₁ε_2... ε_k является свойственной двум или более состояниям в перечне, составленном в (1), то увеличим k на 1 и возвратимся к (2).

Алгоритм 4.3 может быть продемонстрирован на примере автомата A17 и множества допустимых начальных состояний {2, 3, 4, 5}, для которых мы имеем ε₁ = aa и ε₂ = a. В таблице 4.8 дан перечень реакций на последовательность aaa, разделенную, как сказано в шаге 1. Если оказалось, что начальным состоянием A17 является 2, то реакцией является 00, что может быть свойственно только состоянию 2; следовательно, в данном случае диагностический эксперимент требует только двух входных символов. Если оказалось, что начальным состоянием является 5, то реакция на аа есть 10, что не может быть свойственно одному только состоянию 5 (на основе этого ответа начальным состоянием может быть или 4, или 5), и, следовательно, для того чтобы завершить эксперимент, требуется вторая последовательность.

Очевидно, что всегда, когда диагностическая задача для m состояний может быть решена простым безусловным экспериментом, она всегда может быть решена также простым условным экспериментом, длина которого никогда не превосходит длину безусловного эксперимента и порядок которого никогда не превышает m. — 1. Преимущество такого условного эксперимента заключается в том, что он может закончиться раньше, чем безусловный эксперимент. Конечно, точная длина условного эксперимента не может быть оценена заранее, так как она зависит от истинного начального состояния, которое остается неизвестным до тех пор, пока эксперимент не закончится.

Хотя из решения диагностической задачи для т состояний путем проведения простого безусловного эксперимента следует решение путем проведения простого условного эксперимента, обратное неверно. Имеются случаи, когда начальное состояние не может быть распознано никаким простым безусловным экспериментом, но может быть распознано простым условным экспериментом. Примером служит автомат A21 на рис. 4.10 и множество допустимых начальных состояний {1, 2, 3, 4}. Ясно, что любая минимальная диагностическая последовательность для данной задачи должна начинаться с а. Любая последовательность, начинающаяся с аа, дает одинаковые реакции, если A21 находится в состоянии 1 или 2; любая последовательность, начинающаяся с а β, дает одинаковые реакции, если A21 находится в состоянии 3 или 4. Следовательно, не существует последовательности, реакции на которую всех четырех допустимых состояний являются различными. Однако если прикладывается а и затем наблюдается реакция, то имеется возможность определить, находится начальное состояние в {1. 2} (когда реакция равна 0) или в {3, 4} (когда реакция равна 1). Если найдено, что начальное состояние находится в {1, 2}, то может быть приложен символ β, который дает 0, если начальное состояние есть 1, и 1, если начальное состояние есть 2; если найдено, что начальное состояние находится в {3, 4}, то может быть приложен символ а, который дает 1, если начальное состояние

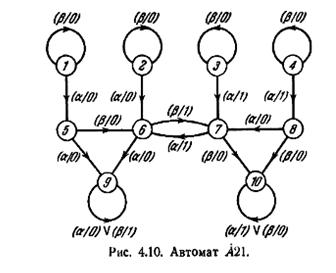
есть 3, и 0, если начальное состояние есть 4. Таким образом, начальное состояние может быть распознано с помощью простого условного эксперимента порядка 2 и длины 2. В заключение имеем следующую теорему.

Теорема 4.4. Каждая диагностическая задача для т состояний, которая может быть решена с помощью простого безусловного эксперимента длины l, может быть также решена с помощью простого условного эксперимента длины l или меньше и порядка m — 1 или меньше. Имеются диагностические задачи для m состояний, которые не могут быть решены с помощью простого безусловного эксперимента, но могут быть решены с помощью простого условного эксперимента.

Условный эксперимент, описанный алгоритмом 4.3, по существу, является безусловным экспериментом со способностью к раннему завершению, основанной на наблюдении реакций. Поэтому такой условный эксперимент зависит от существования безусловного эксперимента и ни в коем случае не является общим. Более общим условным экспериментом является эксперимент, в котором после приложения любого входного символа на основе наблюдаемой реакции исключается как можно больше допустимых состояний, т. е. рассматриваются только те допустимые состояния, которым

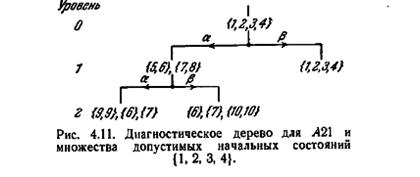
могут быть приписаны прошлые реакции. В терминах дерева преемников это означает, что путь, который ведет к A-группе, содержащей кратное σ-множество, может быть еще использован для построения диагностического эксперимента, так как кратное σ-множество может быть получено из допустимых состояний, которые были ранее исключены. Этот факт демонстрируется диагностическим деревом для автомата A21 и множества допустимых начальных состояний {1, 2, 3, 4}, показанным на рис. 4.11. Хотя пути, описывающие аа и а β, ведут к A-группам, содержащим кратные σ-множества {9, 9}

и {10, 10} соответственно, эти σ-множества могут быть исключены на основе реакции на первый символ а; после того как приложено а, могут быть исключены или состояния 1 и 2, как допустимые состояния (в этом случае можно пренебречь {9, 9}), или состояния 3 и 4 (в этом случае можно пренебречь {10, 10}).

Обобщая предыдущие замечания, можно отметить, что простой условный эксперимент для автомата М и его множества допустимых начальных состояний

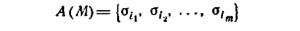
может быть реализован, если дерево преемников для М и А(М) содержит m путей, природа которых указана на рис. 4.12. На этом рисунке σ´i_h обозначает преемника σ´i_h; любой из m путей, показанных на рисунке, может полностью перекрывать какой-либо из остальных путей, В добавление

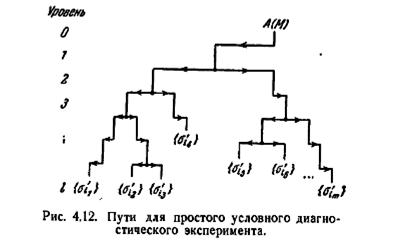
к таким путям простой условный эксперимент требует ряда правил: (1) правило для выбора первого входного символа в эксперименте; (2) правило выбора (k + 1)-го входного символа в эксперименте при условии, что дана реакция на предыдущие k символов; (3) совокупность правил, которые должны давать в результате входную последовательность, описываемую путем, заканчивающимся в {σ´i_h} (h =1, 2,..., m), если истинное начальное состояние есть состояние σ´i_h из А(М).

Посредством доказательства, подобного доказательству леммы 4,4, может быть показано, что если множество путей длины (m — 1)n^m или меньшей не имеет свойств, отмеченных на рис. 4.12, то никакое множество путей любой длины не имеет этих свойств. Таким образом, мы имеем следующую теорему. Теорема 4.5. Если диагностические задачи для автомата с n состояниями и m допустимыми состояниями вообще могут быть решены путем проведения простого условного эксперимента, то они могут быть решены с помощью простого условного эксперимента длины l, где

l ≤(m -1)n^m. (4.6)

Для того чтобы определить, может ли быть реализован простой условный эксперимент для заданных М и А (М), определяют сначала, существует ли требуемое множество путей. Если это так, то составляют перечень всех возможных совокупностей правил для выбора входной последовательности. Если существует совокупность правил, которые выполняют оговоренные выше условия (1), (2) и (3), то такой эксперимент существует, и эта совокупность может быть использована для его выполнения. Если совокупность правил, удовлетворяющая этим условиям, не существует, то диагностическая задача для М и А (М) не может быть решена с помощью простого условного эксперимента. По теореме 4.4, из этого следует, что задача не может быть решена никаким простым экспериментом — безусловным или условным.

Чтобы убедиться в том, что имеются случаи, когда диагностическая задача не может быть решена никаким простым экспериментом — безусловным или условным, рассмотрим автомат A21 на рис. 4.10 и множество допустимых начальных состояний {5, 6, 7, 8}. Любая последовательность или подпоследовательность, начинающаяся с а, заставляет состояния 5 и 6 перейти в состояние 9 с одинаковыми реакциями; любая последовательность или подпоследовательность, начинающаяся с β, заставляет состояния 7 и 8 перейти в состояние 10 с одинаковыми реакциями. Следовательно, уже после приложения первого входного символа (для того чтобы начать безусловный или условный эксперимент) нет возможности когда-либо различить состояние 5 и 6 или состояние 7 и 8. Таким образом, мы имеем следующую теорему.

Теорема 4.6. Имеются диагностические задачи для т состояний, которые не могут быть решены ни с помощью простых безусловных экспериментов, ни с помощью простых условных экспериментов.