Установочное дерево

Установочное дерево, как и диагностическое дерево, есть усеченный вариант дерева преемников, полученный путем применения ряда правил завершения.

Определение 4.2. Установочное дерево есть дерево преемников, в котором ветвь b k-то уровня становится оконечной, если выполняется одно из следующих условий: (1) A-группа, связанная с b, является связанной с некоторой ветвью в уровне, предшествующем k-му. (2) Имеется ветвь k-го уровня (возможно, сама b), связанная с однородной A-группой.

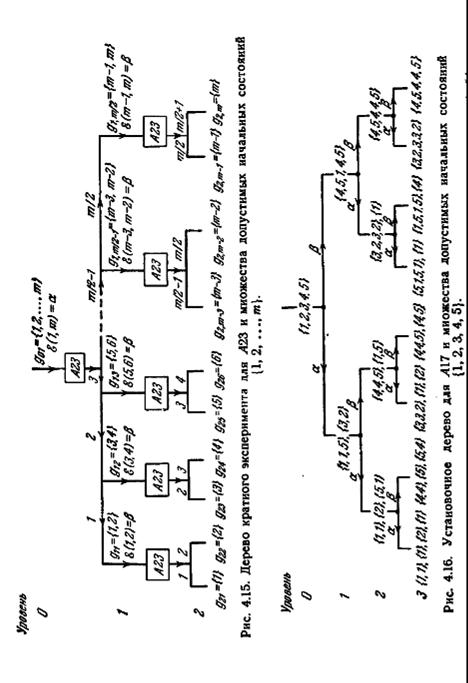
Правило (2) подразумевает, что первый уровень, который содержит ветвь, связанную с однородной A-группой, также является последним уровнем в установочном дереве. Рис. 4.16 демонстрирует, как строится установочное дерево для автомата A17, представленного на рис. 4.3, и множества допустимых начальных состояний {1, 2, 3, 4, 5}. Очевидно, что в третьем уровне A-группа {1, 1}, {1}, {2}, {1} является однородной; поэтому в силу правила 2 все ветви в третьем уровне являются оконечными.

Посредством доказательства, аналогичного доказательству, примененному в лемме 4.4, можно показать, что длина любого пути в установочном дереве для автомата M с n состояниями и т допустимыми состояниями не может превышать (m — 1)n^m. Поэтому построение установочного дерева есть конечный процесс. В следующем параграфе будет получена граница, которая существенно ниже, чем (m—1)n^m.

Установочным путем будет любой путь в установочном дереве, оконечная ветвь которого связана с однородной A-группой. Установочной последовательностью для М и А(М) будет любая входная последовательность, которая, будучи приложенной к М|σ_i и M|σ_j, где σ_i и σ_j суть два состояния в А(М), дает две различные выходные последовательности, если она переводит σ_i и σ_j в два различных состояния. Тогда лемма 4.2 дает следующую лемму.

Лемма 4.7. Входная последовательность, описываемая установочным путем в установочном дереве, построенном для М и А(М), есть установочная последовательность для М и А(М).

Минимальная установочная последовательность для М и А(М), обозначаемая через ε´(А), есть кратчайшая установочная последовательность для М и А(М). Усеченные пути установочного дерева, построенного для М и А(М), суть пути, включенные в дерево преемников, но отсутствующие в установочном дереве в силу правила 1. Следующий результат может быть доказан способом, целиком аналогичным способу, примененному в лемме 4.6.

Лемма 4.8. Усеченные пути установочного дерева, построенного для М и А(М), не описывают минимальных диагностических последовательностей.

Таким образом, мы имеем следующую теорему — аналог теоремы 4.2.

Теорема 4.10. Множество последовательностей, описываемых установочными путями в установочном дереве, построенном для автомата М и множества допустимых начальных состояний А (М), есть множество всех минимальных установочных последовательностей для М и А (М).