Все алгебры можно классифицировать с точки зрения свойств операций, заданных на множествах-носителях. Эта классификация позволяет выделить из множества алгебр алгебры определенного рода, которые будут одинаковы, с точностью до изоморфизма.
Прежде, чем давать определения различных родов алгебр, договоримся о терминологии. Если задана бинарная алгебраическая операция на множестве А, то в зависимости от того, какая задана операция и как она обозначена, будем говорить и писать:
| В общей терминологии | В аддитивной терминологии | В мультипликатив-ной терминологии |
| Операция * | Сложение + | Умножение • |
| Результат a * b | Сумма a + b | Произведение a • b |
| Нейтральный элемент е | Нуль 0 | Единица 1 |
| Симметричный элемент a' | Противополож-ный элемент -a | Обратный элемент a-1 |
Определение 1. Алгебра <А, *> с одной бинарной операцией называется группоидом.
Например, <N, •>, <Z. - >, <Q\{0},:> - группоиды, a <N, +, •>, <N, ->, <Z,:>. <Q,:> - не являются группоидами.
Определение 2. Полугруппой называется алгебра <А, *> с бинарной ассоциативной операцией:
" a,b,cÎ А, (а*b)*с = а*(b*с). Можно сказать, что полугруппа - это ассоциативный группоид.
Например, <N, •>. < Z, +>, <Q, +> - полугруппы, так как операции сложения и умножения на множествах N, Z, Q - ассоциативны. Алгебры <Z, ->, <Q\{0},:> не являются полугруппами.
Определение 3. Моноидом называется алгебра <А, *>, бинарная операция которой удовлетворяет условиям:
1) " a,b,c Î А, (а*b)*с = а*(b*с) - операция ассоциативна,
2) $ е ÎА | " a Î A, е*а = а*е = а - существует нейтральный элемент.
Можно сказать, что моноид - это полугруппа с нейтральным элементом.
Например, <Z, •> - является моноидом, так как е = 1, 1 ÎZ, a <N, +> не является моноидом, так как е=0, 0ÏN.
Определение 4. Группой <G. *> называется алгебра, бинарная операция которой удовлетворяет условиям, называемым также аксиомами группы:
Аl. " a,b,cÎ G, (a*b)*c = a*(b*c) (ассоциативность);
А2. $ е Î G | "aÎG, e*a = a*e = а (существование нейтрального элемента);
A3. " a Î G, $ a' Î G | a*a' = a'*a = e (симметризуемость каждого элемента).
Из определения видно, что любая группа является полугруппой и моноидом. Можно сказать, что группа - это моноид, каждый элемент которого имеет симметричный элемент.
В некоторых случаях, удобно использовать следующее определение группы:
Определение 4*. Алгебра <G, *> с бинарной операцией * называется группой, если выполняются следующие условия:
а) " a,b,c Î G, (a*b)*c = a*(b*c).
б) " a,b Î G, каждое из уравнений а*х = b и у*а = b имеет хотя бы одно решение.
Первое определение группы более удобно для проверки того факта, будет ли данная алгебра группой. Второе определение характеризует группу как алгебру, в которой разрешимы уравнения первой степени. Можно доказать, что определения 4 и 4* равносильны. В определении группы заложен алгоритм решения всех задач, связанных с выяснением вопроса - будет ли данная алгебра группой.
Определение 5. Группа <G, *> называется коммутативной (или абелевой), если операция * коммутативна, т.е. выполняется аксиома:
А4. " a,b Î G, a*b = b*a (коммутативность).
Указание. Для доказательства того, что множество А с операцией * является группой, нужно.
во-первых, показать, что операция * является бинарной операцией на множестве А, т.е. выполнимой и однозначной операцией ранга 2 на А,
во-вторых, проверить выполнимость аксиом A1, A2, A3 группы для алгебры <А, *>.
Если первое из этих условий не выполняется, то нет смысла в проверке аксиом.
Пример 1. Рассмотрим множество Z целых чисел относительно операции сложения. Покажем, что <Z, +> - абелева группа.
а) Операция + является выполнимой на Z, так как " a,bÎZ, (a+b)ÎZ; однозначной на Z, так как результат (а + b) определяется однозначно. Ранг операции "+" равен двум, так как в определении операции используется пара элементов (а, b) ® (а + b). Следовательно, <Z, +> - группоид.
б) Операция "+" ассоциативна на Z, так как " a,b,cÎ Z,
(а+b)+с = а+(b +с). Следовательно, <Z, +> - полугруппа.
в) Роль нейтрального элемента будет играть число 0, так как
" a Î Z, а + 0 = 0 + а = а. Следовательно, <Z, +> - моноид.
г) Для всякого целого числа существует противоположное число: " aÎZ, $ (-а) | а + (-а) = (-а) - а = 0.
Следовательно, <Z, +> - группа.
д) Операция + коммутативна на Z, так как " a,b Î Z, a + b = b + a.
Таким образом, <Z, +> - коммутативная группа. Ее обычно называют аддитивной группой целых чисел.
Пример 2. Рассмотрим множество Z относительно операции умножения целых чисел. Выясним, алгеброй какого рода является пара <Z, •>:
а) Умножение является бинарной операцией на Z, выполнимой и однозначной. Следовательно, <Z, ·> - группоид.
б) Операция умножения на Z ассоциативна, т.е. " a,b,cÎZ,
a(bc) = (ab)c. Следовательно, <Z, •> - полугруппа.
в) Число 1 является нейтральным элементом относительно операции умножения, так как " a Î Z, 1 • а = а · 1 = а. Значит,
<Z, ·> - моноид.
г) Теперь осталось проверить аксиому существования симметричного элемента на Z относительно операции умножения. Очевидно, что все целые числа, кроме 1 и -1, не имеют обратных элементов на Z, то есть аксиома A3 не выполняется.
Следовательно, <Z, •> - группой не является. Можно также показать, что уравнения ах = b, уа = b разрешимы не для всех целых чисел.
Пример 3. Выясним, будет ли группой множество Q0 рациональных чисел без нуля относительно бинарной операции умножения рациональных чисел.
а) Очевидно, что умножение рациональных чисел является бинарной операцией на Q, выполнимой и однозначной. Следовательно, < Q0, •> -группоид.
б) Операция умножения - ассоциативна. Следовательно,
< Q0, •> -полугруппа.
в) Нейтральный элемент равен 1. Следовательно, < Q0, •> - моноид.
г) Кроме того, " aÎ Q0, $а-1ÎQ0 | а • а-1 = а-1• а = 1.
Итак, < Q0. •> - группа. Ее обычно называют мультипликативной группой рациональных чисел. Очевидно, что группа
< Q0, •> - абелева.
Определение 6. Группу <G, *> называют бе сконечной, если G -бесконечное множество.
Пример 4. Пусть {aк} - множество целочисленных степеней некоторого целого числа а. Тогда <{aк}, •> - бесконечная мультипликативная группа.
Проверьте самостоятельно!
Определение 7. Группу <G, *> называют конечной, если G -конечное множество. Число элементов множества G называют порядком группы и обозначают |G| (или 0r, или (G: 1)).
Пример 5. Рассмотрим пример конечной группы. Пусть дано множество Z и натуральное число m. Будем делить все целые числа на m. Числа, которые при делении на m будут иметь одинаковые остатки, соберем в один класс. Так как различных остатков будет m (0, 1, 2,..., m-1), то и различных классов тоже будет m { 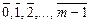 }.
}.
Обозначим это множество классов символом Zm и зададим на этом множестве операцию сложения классов по правилу: 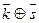 =
= 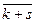
Тогда <Zm, Å > - будет конечной группой. Докажите это самостоятельно!
Пример 6. Доказать, что <Zp0, •>, где р - простое число и 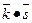 =
= 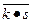 будет тоже группой.
будет тоже группой.
 2015-02-27
2015-02-27 5660
5660