2015-02-27
555
Подстановка t =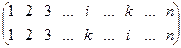 
называется транспозицией элементов (i, k).
Теорема 1. Sg n t= -1 Докажите самостоятельно.
Теорема 2. Алгебра <Sn, o> конечная группа.
Проверьте самостоятельно аксиомы:
1. " j, y, d Î Sn (j ° y) ° d = y ° (j ° d)
2. $ e Î Sn: " j Î Sn (e ° j = j°e = j)
3. " j Î Sn $ j-1 Î Sn: j ° j-1 = j-1 ° j = e
4. |Sn| = n!
Эту некоммутативную группу называют симметрической группой подстановок степени (n) и обозначают sn=<Sn, O>
Обозначим через An - множество всех четных подстановок группы sn
Теорема 3. <Аn, °> - подгруппа группы sn, ее называют знакопеременной группой подстановок n-ой степени.
Докажите самостоятельно.
Определение 6. Определителем (детерминантом) n-го порядка квадратной матрицы А = ||aik||, i, к=1, 2, 3,...,n называют сумму вида:
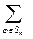Sgn j a1j(1) × a2j(2) × …anj(n) , где Sn =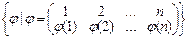 
Sgn j =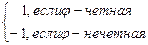 
Обозначается эта сумма короче символами det A или |А|. Если это определение проговорить словами, то получится следующее:
«Определителем n-го порядка квадратной матрицы А называют алгебраическую сумму всевозможных членов, каждый из которых представляет собой произведение n-элементов, взятых по одному и только одному разу из каждой строки и каждого столбца матрицы А, знак любого члена определяется четностью (нечетностью) подстановки его индексов».
|
|
|
Непосредственно из определения определителя n-го порядка следует истинность следующих утверждений:
1. Определитель n-го порядка имеет n! членов.
Действительно, суммирование введется по всем подстановкам jÎSn, а множество Sn имеет ровно n! членов, так как на множестве М = {1, 2,...,n} из n элементов можно задать n! подстановок (каждая подстановка является биекцией j: М ®М).
2. Половина членов определителя будет иметь знак (+), половина - (-), так как половина подстановок будут четными, половина - нечетными.
3. Определитель, в котором какая-то строка или столбец нулевые, будет равен нулю.
Действительно, в этом случае каждый член определителя
a1j(1) ×a2j(2) ×…anj(n) в качестве одного из сомножителей будет содержать ноль.
4. Если все элементы какой-либо строки (столбца) определителя n-го порядка имеют общий множитель, то его можно вынести за знак определителя (суммы).
Действительно, тогда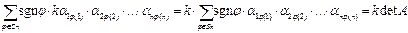 
Используя определение детерминанта n-го порядка, найдем разложение определителя 3-го порядка.
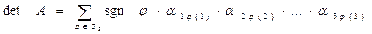
Матрица А=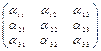 
S3 =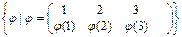 
Найдем все подстановки из множества S3 и определим их четность.
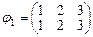- четная; 
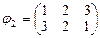- нечетная;
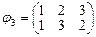- нечетная; 
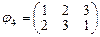- четная;
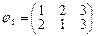- нечетная; 
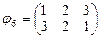- четная;
Теперь запишем разложение определителя 3-го порядка:
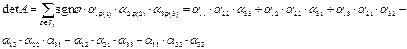Из этого разложения видно, что члены со знаком "+" и со знаком "-" выбираются по схемам, которые носят название "'Правило Саррюса".
Пример 4: Вычислить определитель:
|
|
|
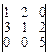=1•1•5 +2•2•0 + 3•0•0 - 0•1•0 -3•2•5 -0•2•1=5 -30= -25
Опираясь на определение детерминанта, можно записать его разложение для порядка n = 4, n = 5,... Но при этом число членов определителя будет стремительно возрастать.
При n = 4 определитель будет иметь 4! = 1•2•3•4 = 24 члена, при n = 5 уже 5! = 1•2•3•4•5 = 120 членов, при n = 6,
6! = 1•2•3•4•5•6 = 120 • 6 = 720 членов и т.д. Поэтому определители порядка выше n = 3 вычисляют, опираясь не на его определение, а на его свойства.
Основную роль при этом играет такое свойство: элементарные преобразования над строчками (столбцами) определителя n-го порядка не изменяют его значения. Поэтому определитель любого порядка с элементами из поля R может быть приведен к так называемому «треугольному» виду:
Например:
а) det A =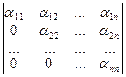 
= 
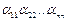
б) det A=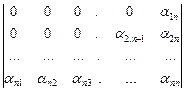 
= 
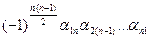
в)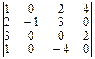 
= 
= 
= = 
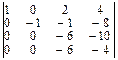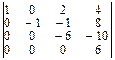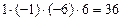
Понятия минора и алгебраического дополнения элемента aik определителя n-го порядка позволяют вычислять определители путем разложения их по строке или столбцу, а так же понижать порядок определителя.
Определение 7. Минором Mik элемента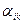 
определителя
n-го порядка называется определитель (n-1) порядка, который получается из данного определителя путем вычеркивания i - й строки и k - гo столбца.
Определение 8. Алгебраическим дополнением Aik элемента aik определителя n-го порядка называют минор Mik, взятый со знаком (-1)i+к, т.е. Аik = (-1)i+к Mik,
Пример 5. Вычислить А23 элемента a23 определителя |А| = =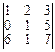 
1. Находим минор M23 элемента a23. Дня этого вычеркиваем вторую строчкуи третий столбец, получаем определитель:
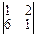= 1 - 12 = -11
2. Итак. М23 = -11. Тогда А23 = (-1)2+3М23 = -М23 =11
Теорема 4. Докажите,
что det A =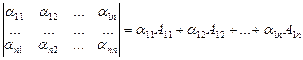 
(самостоятельно).
