Глава 3. Системы линейных уравнений, методы их решения

Основными понятиями этой темы служат понятия: система линейных уравнений, ее расширенная матрица, элементарные преобразования систем и матриц, их взаимосвязь.

Определение 1. Системой (s) линейных уравнений с (n) переменными называется система вида:

1)

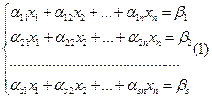
где a_ik ÎR (i=1, 2,..., s) (k=1, 2,..., n)

2) Систему (1) можно записать короче в виде: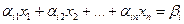

i = 1, 2,...,s, a_ik называют коэффициентами, x₁,x₂,…,x_n - переменными, b_i- свободными членами, a₁₁x₁,…, a_snx_n - членами уравнений.

Определение 2. Решением системы уравнений (1) называется набор чисел (l₁,l₂,...,l_n)таких, что при их подстановке соответственно вместо x₁, x₂,.., x_n каждое уравнение системы обращается в верное равенство.

В этом случае говорят, что набор (l₁,l₂,...,l_n) удовлетворяет системе (1). Решить систему - это значит найти все ее решения (или доказать, что их не существует).

Определение 3. Две системы уравнени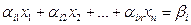й

и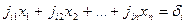

называются равносильными (эквивалентными), если каждое решение одной системы является решением другой, и обратно: каждое решение второй является решением первой.

Другими словами, можно сказать, что равносильные системы имеют одно и то же множество решений.

Заметим, что эквивалентные системы могут иметь разное число уравнений. Например,

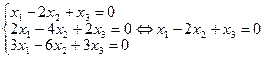
а также то, что две системы, не имеющие решений, будут считаться эквивалентными, исходя из определения 3.

Определение 4. Если система (1) имеет хотя бы одно решение, то она называется совместной, в противном случае - несовместной; если она имеет единственное решение, то она называется определенной, если больше одного решения, то неопределенной.

Определение 5. Элементарными преобразованиями системы линейных уравнений называют следующие преобразования:

1. Перемена местами уравнений системы.

2. Умножение уравнений на число, не равное нулю.

3. Прибавление к одному из уравнений системы другого, умноженного на число.

4. Удаление из системы нулевого уравнения.

Докажите, что всякое элементарное преобразование системы (1) приводит к системе, равносильной данной.

Таблицу А= 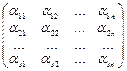называют матрицей системы 1)

Матрицу В= 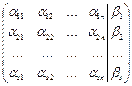называют расширенной матрицей системы 1).

Матрицу В также называют табличной записью системы 1), а запись 1)-полной записью системы. Ясно, что по табличным записям всегда можно воспроизвести полную запись.

Например, пусть

В= 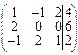, тогда система будет иметь вид: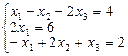

Табличная запись системы 1) более компактна, чем полная запись и более удобна для проведения элементарных преобразований системы линейных уравнений. Например, при умножении уравнения на число все коэффициенты и свободный член умножаются на это число. Следовательно, в табличной записи все элементы соответствующей строки матрицы умножаются на это число. Таким образом, элементарные преобразования системы линейных уравнений можно заменить соответствующими элементарными преобразованиями системы строк расширенной матрицы В.

Теорема 1. Пусть система (1) имеет расширенную ступенчатую матрицу В, ведущие элементы которой 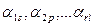, тогда если последний ведущий элемент 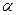_rl удовлетворяет условиям:

1) l=n+1 -система будет несовместной,

2) (l=n)&(r=n) - система будет определённой,

3) (r<n)&(l¹n+1) - система будет неопределённой,

На этой теореме основан универсальный метод решения любой системы линейных уравнений, который называют методом Гаусса или методом последовательного исключения переменных.

Основные шаги алгоритма этого метода:

I. Записывается расширенная матрица В данной системы.

II. Затем матрица В с помощью элементарных преобразований приводится к ступенчатому виду.

III. На основании теоремы определяется решение данной системы.

Пример 1. Решить систему с помощью метода Гаусса.

а)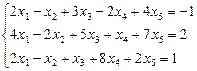

Решение. 1. Записываем матрицу B

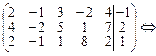
2. Приводим ее к ступенчатому виду

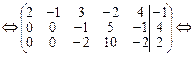
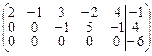
3. Записываем ступенчатую систему на основе полученной ступенчатой матрицы.

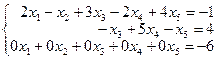
Последнее уравнение системы противоречиво, следовательно, система не имеет решений.

b)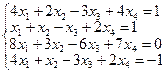

Решение.

Записываем соответствующую данной системе матрицу В и приводим её к ступенчатому виду.

B=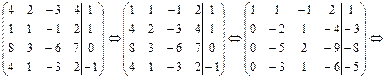

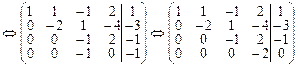
По полученной матрице запишем систему:

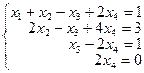
В этом случае система имеет единственное решение (0, 2, 1,0) (проверьте!)

в)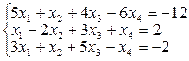

Решение.

B =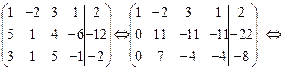

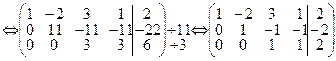
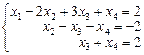
Система имеет множество решений. В этом случае поступают следующим образом: по числу оставшихся уравнений выбирают главные переменные. Пусть это будут х₁ х₂ х₃. Остальные будут свободными, то есть х₄. Выразим главные переменные через свободные (поднимаясь по системе снизу вверх):

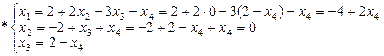
Возьмём для свободного переменного произвольное числовое значение, тогда, снова поднимаясь по системе * снизу вверх, получим однозначно определенные значения для главных переменных. Пусть x₄=1.

Тогда

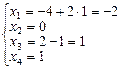
Так как свободным переменным мы можем давать любые числовые значения, то будем получать бесконечное множество решений системы.

Замечание 1. Теорему (1) можно сформулировать в терминах ранга матриц. Действительно, пусть rang А=r₁, rangВ= r₂, где А -матрица системы (1), В - расширенная матрица системы (1)

B =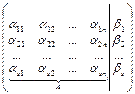

Теорема 1. (Теорема Кронекера-Капелли).

Система: 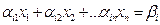где i=1, 2,..., k будет:

1) совместной, если rang A = rang В;

2) совместной и неопределённой, если rang A = rang B < n;

3) несовместной, если rang А ¹ rang В.

Пример 2. Выяснить, совместнали система

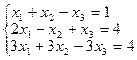
Решение.

Составляем расширенную матрицу В и одновременно находим ранги матриц А и В.

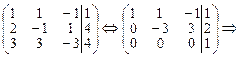RangA=2, RangB=3 Значит, система не имеет решений

Понятие обратимой матрицы лежит в основе матричного метода решения систем линейных уравнений.

В отличие от универсального (общего) метода Гаусса, этот метод имеет существенные ограничения, так как его можно применять лишь для решения систем вида:

1)

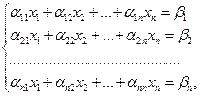
матрица А = ||a_ik||которых должна быть обратима. Тогда систему (1) можно записать в виде матричного уравнения (2) А×Х=В, где

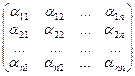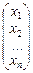А = Х = В =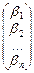

Так как А - обратима, то найдя матрицуА^-1, из уравнения(2) можно выразить матрицуХ= А^-1 В.

Замечание. Здесь важно соблюдать порядок умножения матриц (слева или справа), так как умножение матриц некоммутативно.

Пример 3. Решить систему матричным методом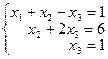

Введём обозначения:

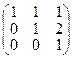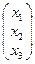А = , Х = , В =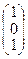

Тогда система в матричной форме будет иметь вид: (*)А×Х=В

Так как rangА=3 и ее порядок 3x3, тo $ А^-1: А^-1 А=А А^-1 = Е. Если равенство (*) домножить слева на А^-1, то получим:

А^-1АХ = А^-1В => Х= А^-1 В

Чтобы теперь найти X, нужно вычислить А^-1 и найти произведение А^-1В.

(A|E)=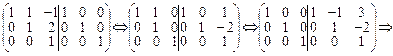

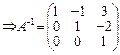
X = 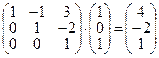x₁ = 4, x₂ = -2, x₃= 1

Проверка:

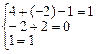
Понятие определителя n-гопорядка позволило разработать ещё один локальный метод решения систем линейных уравнений. Если дана система (n) уравнений с nпеременными

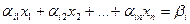где i=1, 2,...,n

и определитель матрицы этой системы отличен от нуля, то есть

|A| ¹0, то решение этой системы можно вычислить по формулам Крамера: 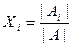i = 1, 2,…, n, где |A| - определитель матрицы А данной системы, а определители |A_i| получаются из определителя |A|путём последовательной замены i-го столбца столбцом свободных членов.

Пример 4. Решить систему методом Крамера:

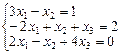
Вычисляем определитель матрицы А этой системы

|A| = 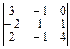= 12-2+0-0-8+3=5

Заменив в этом определителе первый столбец столбцом свободных членов, получим определитель |A₁|

|A₁| = 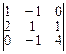= 4+0+0+8+1+0=13

Заменив в определителе |A| второй столбец столбцом свободных членов, получим определитель

|A₂| = 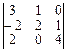= 34

Аналогично находим и вычисляем определитель•

|A₃| = 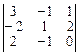= 2

Тогда x₁ = 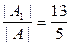; x₂ = 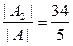; x₃ =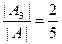

Проверка: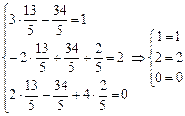

С системой (1) 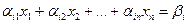где i=1, 2,..., kвсегда можно связать систему (2) 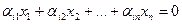, которая называется системой линейных однородных уравнений. Эта система всегда совместна, так как вектор Q = (0, 0,..., 0) является её решением, кроме этого, для этой системы всегда rang A=rangВ, т.к. столбец свободных членов равен нулю. Поэтому, если rang A<n,то система (2) будет иметь множество решений, обозначим его через М.

Теорема 2. áМ,+ {wl| lÎ R.}ñ - является линейным пространством.

Доказательство:

В данном случае не нужно проверять все аксиомы линейного пространства, т.к. решением системы (элементами множества М ) являются арифметические векторы, то достаточно доказать, что М является подпространством Rⁿ .

Для этого нужно взять любые два решения системы (2) и показать, что их сумма будет решением системы (2), а так же произведение любого решения на действительное число снова будет решением системы (2). Действительно: пусть b = (b₁, b₂, …, b_n,) и c = (d₁, d₂, …, d_n,) - решения системы (2). Найдём b + c = (b₁+ d₁, b₂+ d₂,…, b_n+d_n) и подставим в систему (2), получим: a_i1(b₁+ d₁) + a_i2(b₂+ d₂) + …+ a_in(b_n+ d_n) = (a_i1b₁ + a_i2b₂ +…+ a_inb_n) + +(a_i1d₁ + a_i2d₂ +…+ a_ind_n )=0+0=0

Аналогично, lb=(lb₁, lb₂, …, lb_n), a_i1(lb₁)+a_i2(lb₂)+…+a_in(lb_n) = l(a_i1b₁+a_i2b₂ +…+a_inb_n) = l•0 = 0

Итак, áМ,+ {wl| lÎ R.}ñ - линейное пространство.

Базу этого пространства называют фундаментальной системой решений (Ф.С.Р.).

Покажем на конкретном примере алгоритм её нахождения.

Пример 5. Найти Ф.С.Р. для системы:

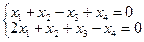
Ре шение.

1 шаг. Методом Гаусса находим общее решение данной системы:

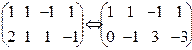
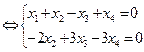
Пусть X₃, X₄ – свободные переменные, X₁, X₂ – главные.

Тогда 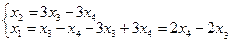- общее решение системы.

2 шаг. Записываем таблицу:

X1	X2	X3	X4
-2
	-3

свободным переменным придаём значения (1,0) и (0,1) и вычисляем главные переменные.

Тогда два вектора C₁ = (-2,3,1,0), С₂=(2,-3, 0, 1) будут базой пространства М (Ф.С.Р.).