Отношение делимости в Z и его свойства

Определение 1. Целое число (а) делится на целое число (b¹0), если $ q Î Z: a=bq

Обозначается: a/b и читается "а делится на b", или "b делит а".

а – делимое,

b – делитель,

q – частное.

Это отношение есть частичная бинарная операция на Z, т.к. 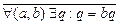. Например, 4 не делится на 3. С другой стороны, это отношение будет трехместным предикатом на множестве Z.

Свойства:

1. Отношение делимости рефлексивно. Действительно: " a Î Z а/а, т.к. $ 1 Î Z: а = а × 1

2. Отношение делимости транзитивно. Действительно:

" a, b, c Î Z (a/b & b/c) => (а/с), т.к. из того что (a/b) Þ

$ q₁ Î Z: a=bq₁, а из того что (b/c) Þ $ q₂ Î Z: b=cq₂, тогда

а = cq₂q₁ = cq₃ => (а/с)

3. Отношение делимости антисимметрично, т.к. " a, b Î Z из того что (а/b & b/а) => [(а= b) v (a = -b)]

Следовательно, отношение делимости не является отношением эквивалентности, а будет отношением частичного порядка на множестве Z.

Определение 2. Целое число (а) делится на (bÎZ & b¹0) с остатком, если $ q, r Î Z: а = bq + r, где 0 < r < |b| а – делимое.

b – делитель, q - неполное частное, r — остаток.

Замечание 1. Из определения следует, что остаток всегда число неотрицательное.

Пример 1. Разделить - 49 на 17. Получим: - 49 = 17 • (-3)+2

Теорема 1. В кольце Z любое целое число (а) можно разделить на целое число (b¹0) с остатком, единственным образом.

1. Покажем возможность деления.

Пусть bq - наибольшее кратное числа b, которое не превосходит (а), тогда bq £ а £b(q+l) => 0£ a-bq £ b положим, что a-bq = г, тогда получим, что а = bq + r, где 0< r <|b|.

2. Докажем единственность такого представления. Предположим противное,

Пусть a=bq₁+r₁, 0<r₁<|b| и а= bq₂+r₂ 0< r₂ <|b| =>

=> b(q₁ -q₂) = (r₁-r₂) => (r₂-r₁)/b, а т.к. |r₂-r₁|<|b| =>

=> (r₂-r₁) = 0 => (r₂ = r₁)

Т.к. b¹0 то из равенства b(q₁-q₂) = 0 => (q₁-q₂) = 0 => (q₁ = q₂).