Содержание темы.
Теорема о существовании поля комплексных чисел. Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, тригонометрическая форма записи, действия над комплексными числами в тригонометрической форме.
Основные умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:
- уметь изображать комплексные числа на координатной плоскости в виде точек и радиус-векторов и наоборот;
- уметь находить модуль и аргумент "zÎC, переходить от алгебраической формы записи комплексного числа к тригонометрической и наоборот;
- уметь выполнять арифметические операции над комплексными числами в алгебраической и тригонометрической форме, понимать их геометрический смысл;
- использовать полученные знания при решении задач алгебры и геометрии.
Все теоретические положения и практические выводы этой темы вытекают из теоремы о существовании поля комплексных чисел.
Теорема 1: Существует единственное, с точностью до изоморфизма, поле С, в котором выполняются следующие условия:
1. Поле R является подполем поля С.
2. i2 = -1
3. "zÎC $х, yÎR: z = x+ iy
Запись комплексного числа zв виде х + iy называется его алгебраической формой, при этом (х) называют действительной частью комплексного числа, iy - мнимой частью, а (у) – коэффи-циентом мнимой части. Обозначение: Re z - действительная часть, Im z - мнимая часть комплексного числа.
Так как (z = х + iy) Î (C = R x R), то с геометрической точки зрения, любое комплексное число имеет две равноправные геометрические интерпретации (модели).
а) точка координатной плоскости А (х, у);
б) радиус-вектор  с концом в точке с координатами (х, у)
с концом в точке с координатами (х, у)
Геометрический подход к понятию комплексного числа позволяет записывать его в так называемой тригонометрической форме.
Для этого вводятся понятия модуля и аргумента комплексного числа.
Определение 1: Модулем комплексного числа z называется арифметическое значение корня квадратного из х2 + у2, то есть
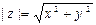
Это понятие является обобщением понятия «абсолютная величина действительного числа», так как, если z = х + 0i, то 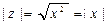 .
.
С геометрической точки зрения, модуль комплексного числа - это длина радиус-вектора ОА или расстояние от начала координат до точки с координатами (х, у).
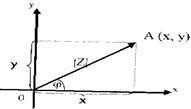
Определение 2: Аргументом комплексного числа z называют угол j между положительным направлением оси 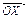 и радиус - вектором
и радиус - вектором 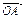 , отсчитываемым против часовой стрелки.
, отсчитываемым против часовой стрелки.
Из этого определения следует, что аргумент комплексного числа определяется неоднозначно, а с точностью до числа, кратного 2p. Поэтому на практике, в качестве аргумента, обычно берут наименьший положительный или наименьший по абсолютной величине угол, который обозначают j =arg z и находят из соотношений:
cos j = 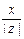 , sin j =
, sin j = 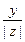 , 0 £ j £ 2p
, 0 £ j £ 2p 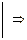
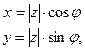
тогда х + iy = 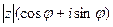 и мы получим тригонометрическую формулу записи комплексного числа.
и мы получим тригонометрическую формулу записи комплексного числа.
Во избежание ошибок при нахождении аргумента комплексного числа z его нужно предварительно изобразить на координатной плоскости.
Модуль и аргумент комплексного числа z являются известными из курса геометрии полярными координатами точки, соответ-ствующей числу z. При этом полярной осью служит ось 
Понятие модуля и аргумента комплексного числа z позволяют записать это число в тригонометрической форме.
Пример 1. Комплексное число z = 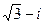 записать в тригонометрической форме.
записать в тригонометрической форме.
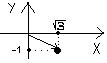
1. Изобразим данное комплексное число на координатной плоскости. Это будет радиус-вектор с концом в точке (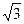 , -1) (см. рисунок)
, -1) (см. рисунок)
2. Найдем его модуль | z | = | 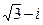 | =
| = 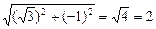
3. Найдем аргумент из соотношений
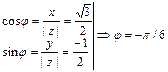 или j = 11p/6
или j = 11p/6
Таким образом,
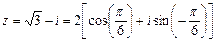
Существование двух форм записи одного и того же комплексного числа z = х + iy = |z| (cosj + sinj) позволяет выполнять алгебраические операции на множестве С в той форме, которая наиболее удобна в каждом конкретном случае.
Теорема 2. Если z1 =x1 + iy1, z2 =x2 + iy2, то
1. z1+z2 = (x1+x2) + i(y1+y2)
2. z1-z2 = (x1-x2) + i(y1-y2)
3. z1×z2 = (x1x2 -y1y2) + i(x1y2 + x2 y1)
4. 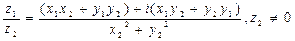
5. 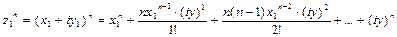 На практике обычно формулы 3), 4) не запоминают, а руководствуются такими мнемоническими правилами:
На практике обычно формулы 3), 4) не запоминают, а руководствуются такими мнемоническими правилами:
а) чтобы перемножить два комплексных числа, нужно перемножить их как два двучлена;
б) чтобы разделить z1 на z2 ¹ 0, нужно числитель и знаменатель домножить на комплексное число, сопряженное знаменателю и выполнить указанные действия (z = х – iy называют сопряженным по отношению к z = х + iy).
Извлечение  в алгебраической форме практически не используется.
в алгебраической форме практически не используется.
Пример 2. z1 = -2 + 5i, z2 = 1 + 3i
z1 + z2= -1 + 8i
z1 - z2= -3 + 2i
z1• z2 = (-2 + 5i)(1 + 3i) = (-2 - 6i + 5i + 15i2) = -17 – i
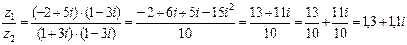
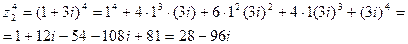
Теорема 3. Если z1=|z1|(cosj+i sinj), z2=|z2|(cosy+i siny), то
1) z1•z2= |z1| |z2| [cos(j+y) + i sin (j+y)]
2) z1n = |z1|n [cos(nj) + i sin (nj)]
3) 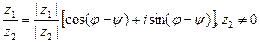
4) 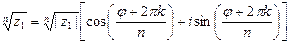 k = 0,1, 2,.., (n-l)
k = 0,1, 2,.., (n-l)
Операции сложения и вычитания в тригонометрической форме на практике не выполняются.
 2015-02-27
2015-02-27 1261
1261
