Пример 3

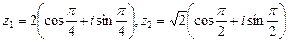
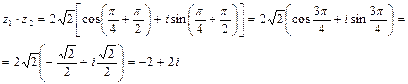
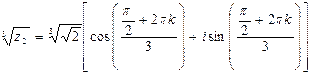k = 0, 1, 2

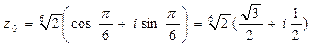
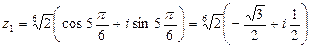
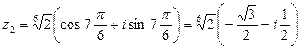
Операции над комплексными числами также могут быть осмыслены с геометрической точки зрения. Так, операциям сложения и вычитания двух комплексных чисел соответствуют операции сложения и вычитания двух векторов по правилу параллелограмма.

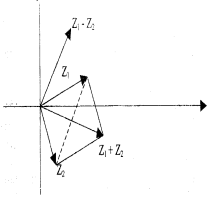
рис.1

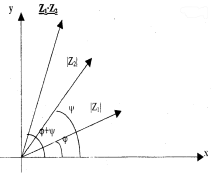
рис. 2

Пример 4. Пусть z₁ = 3 + i, z₂ = 1 – 3i. Найти z₁ + z₂ и z₁ - z₂ геометрически.

Изображаем каждое комплексное число в виде радиус-вектора, затем строим параллелограмм и находим вектор, соответствующий z₁ + z₂ и z₁ - z₂ (см. рис.1)

Геометрический смысл произведения двух комплексных чисел можно выяснить, если перемножить эти числа в тригонометрической форме. Пусть Z₁ = |Z₁|(cosj + i sinj), Z₁ ¹ 0,

Z₂ = |Z₂| (cosy + i siny), Z₂ ¹ 0, тогда

z₁ × z₂ = |z₁|×|z₂| [cos(j + y) + i sin(j+ y)]

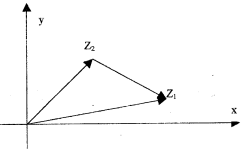
При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, аргументы складываются. Следовательно, чтобы умножить комплексное число z₁ на z₂ нужно длину вектора z₁изменить в |z₂| раза (растянуть или сжать), а затем полученный вектор повернуть вокруг начала координат на угол arg z₂ (см. рис. 2).

Геометрический смысл операции 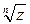состоит в делении окружности радиуса 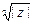на n равных частей.

Пример 5. Вычислить 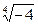и изобразить все его значения геометрически.

Представим комплексное число z = - 4 в тригонометрической форме. Для этого найдем его модуль и аргумент. |-4|=4arg(-4)=p, -4 = 4 (cosp + i sinp)

Тогда 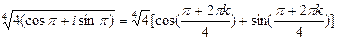k = 0,1,2,3

Придавая параметру (k) значения 0, 1,2, 3, получим четыре значения корня четвертой степени из -4.

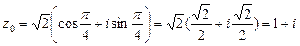
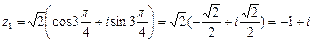
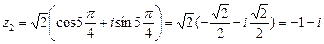
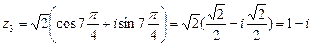
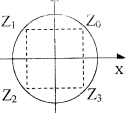Изобразим найденные корни на комплексной плоскости, они делят

окружность радиуса Ö2 на четыре равные части. Кроме этого, мы вписали в эту окружность правильный четырех-угольник (квадрат).

Часто при решении задач используется геометрический смысл модуля разности двух комплексных чисел, как расстояния между двумя точками на плоскости. |z₁ - z₂| = r(z₁, z₂)

Задача 1. Найти геометрическое место точек, для которых |z - (2 + i)| < 3

Геометрический смысл этого неравенства состоит в том, что расстояние от точки (2, 1) до точек (х, у) не должно быть больше трех единиц.

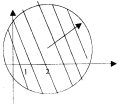
Это значит, что искомым геометрическим местом точек является открытый круг (точки окружности ему не принадлежат) с центром в точке (2, 1) и радиусом r = 3

Этот ответ на вопрос задачи можно было получить и алгебраически, используя определение модуля

|(x + iy) - (2 + i)| < 3 Þ |(x- 2) + i(y -1)| < 3 Þ

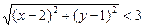Þ (x-2)² + (y-l)²<9

Из курса геометрии известно, что равенство (х-2)²+(у - 1)²=3² есть уравнение окружности с центром в точке (2, 1) и r = 3, тогда искомым г.м.т. будет внутренняя часть этого круга.