Решение систем линейных уравнений методом Жордана-Гаусса

Алгоритм метода Жордана- Гаусса:

1 шаг. Рассмотрим одно из уравнений системы (1), назовем его разрешающим.

2 шаг. В этом уравнении выберем любое неизвестное с ≠ 0 коэффициентом (если есть возможность, то равным 1), назовем этот коэффициент разрешающим элементом.

3 шаг. Исключим выбранное неизвестное из всех уравнений, кроме разрешающего уравнения.

4 шаг. Повторяем шаги 1-3 для всех уравнений системы. Каждое уравнение должно быть разрешающим только один раз. После конечного числа шагов определяем решение системы или устанавливаем ее несовместность.

Процесс решения проводится в таблицах. Переход от одной таблицы к другой осуществляется по правилам:

1. Разрешающая строка делится на разрешающий элемент.

2. Разрешающий столбец дополняется нулями.

3. Если в разрешающей строке (столбце) имеются нули, то соответствующие им столбцы (строки) переписываются без изменения.

4. Остальные элементы вычисляются по правилу «прямоугольника».

4.Метод Гаусса.

Одним из наиболее удобных методов решения системы линейных уравнений является метод последовательного исключения неизвестных или метод Гаусса.

Пусть дана система (1).

Разделим первое уравнение системы на 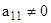, получим

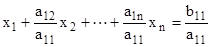
Это уравнение умножим на 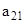и вычтем из второго, затем те же операции проделаем над всеми остальными уравнениями системы. С помощью таких операций исключим 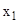из всех последующих уравнений, начиная со второго, т.е. получим 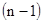уравнений не содержащих 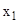. Аналогичным образом с помощью одного из уравнений полученной системы исключим неизвестное x 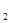и т.д. Систему (1) приведем к треугольному виду:

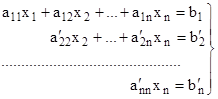
Определитель системы 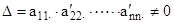. Из последнего уравнения определим 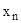, подставив его значение в предпоследние уравнение, определим 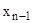, и т.д. до первого уравнения из которого определим .

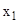С практической точки зрения процесс решения облегчится, если проделать все элементарные преобразования с расширенной матрицей.

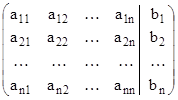
Две системы линейных уравнений называются эквивалентными или равносильными, если каждое решение первой системы является решением второй и наоборот. Соответствующие расширенные матрицы также являются эквивалентными.

Теорема 1. При элементарных преобразованиях система линейных уравнений преобразуется в равносильную.

ВЕКТОРЫ И СИСТЕМЫ ВЕКТОРОВ

Цель лекции: Рассмотреть прямоугольную систему координат на плоскости и в пространстве; понятие вектора. Научить выполнять действия над векторами.

Ключевые слова: координаты точки на плоскости и в пространстве, радиус – вектор, координатная форма вектора.

План лекции

1. Линейные операции над векторами.

2. Скалярное произведение векторов и его свойства.

3. Линейная зависимость и независимость векторов.

4. Базис и ранг системы векторов.

5. Линейные операторы.

6. Собственные векторы и собственные значения линейного оператора.