Рассмотрим звено, дифференциальное уравнение которого
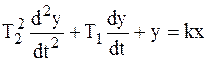 . .
| (2.40) |
Переходя к изображениям, получаем:
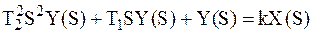 . .
| (2.41) |
Тогда
 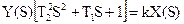 . .
| (2.42) |
Отсюда передаточная функция
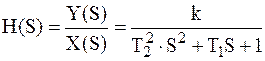 . .
| (2.43) |
Переходная характеристика:
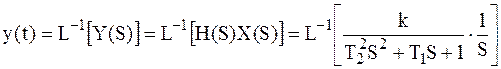 . .
| (2.44) |
Найдем корни уравнения:
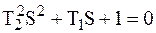 . .
| (2.45) |
Или, что равносильно:
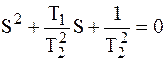 . .
| (2.46) |
Решение квадратного уравнения, как известно,
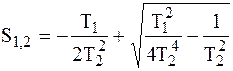 . .
| (2.47) |
Отсюда дискриминант уравнения:
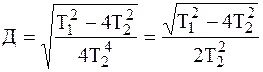 . .
| (2.48) |
Здесь возможны три случая:
Первый случай
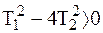 , ,
| (2.49) |
т.е.
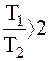 . .
| (2.49а) |
В этом случае уравнение (2.45) имеет два действительных корня 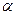 и
и 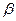 . Тогда переходная характеристика
. Тогда переходная характеристика
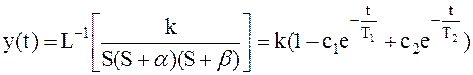 , ,
| (2.50) |
где
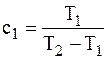 ; ; 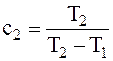 ; ;
| (2.50а) |
График функции (2.50) имеет вид, представленный на рис. 2.10.
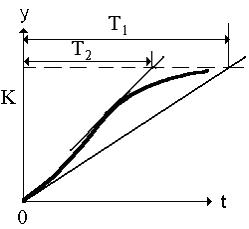
Рисунок 2.10 – Переходная характеристика инерционного
звена второго порядка
Эта характеристика очень напоминает характеристику, представленную на рис. 2.9, и отличается от нее перегибом в начальной части. Такую характеристику называют характеристикой инерционного звена второго порядка.
Второй случай
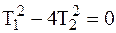 , ,
| (2.51) |
т.е.
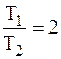 . .
| (2.51а) |
В этом случае переходная характеристика
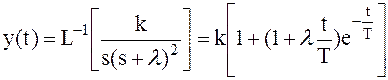 . .
| (2.52) |
По внешнему виду она мало отличается от характеристики, приведенной на рис. 2.10, т.е. и в этом случае мы имеем дело с инерционным звеном второго порядка.
Третий случай
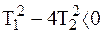 , ,
| (2.53) |
т.е.
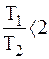 . .
| (2.53а) |
В этом случае уравнение имеет комплексные корни. Пусть 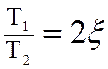 . Тогда знаменатель передаточной функции (2.43)
. Тогда знаменатель передаточной функции (2.43)
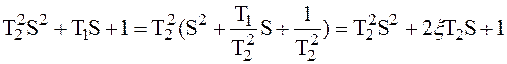 , ,
| (2.54) |
где 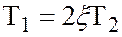 , а
, а 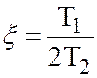 .
.
 2015-02-27
2015-02-27 340
340








