Статически определимыми называются такие задачи, которые можно решить методами статики твердого тела, т.е. задачи, в которых число неизвестных не превышает числа уравнений равновесия.
Статически неопределимыми называются задачи с числом неизвестных, превышающих число уравнений равновесия, т.е. задачи, которые нельзя решать методами статики твердого тела и для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками.
Приведем несколько примеров статически неопределимых задач:
1) балка, закрепленная на концах неподвижными цилиндрическими шарнирами (рис.5.9).
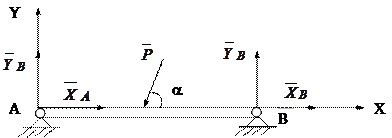 |
Рис.5.9.
Здесь число неизвестных реакций 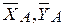 ,
, 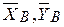 - четыре, тогда как для плоской системы сил, приложенных к твердому телу, можно составить только 3 уравнения равновесия.
- четыре, тогда как для плоской системы сил, приложенных к твердому телу, можно составить только 3 уравнения равновесия.
2) Подвеска, состоящая из трех не лежащих в одной плоскости тросов (рис.5.10).
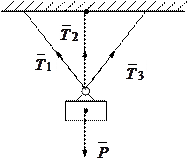 |
Рис.5.10.
Здесь число неизвестных реакций (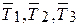 )- три, но система сил, приложенных к подвеске является плоской сходящейся, поэтому уравнений равновесия будет только два, что будет недостаточно для определения всех неизвестных.
)- три, но система сил, приложенных к подвеске является плоской сходящейся, поэтому уравнений равновесия будет только два, что будет недостаточно для определения всех неизвестных.
|
|
|
3)Сочлененная система двух тел, представленная на рис.5.11.
Расчленяя эту конструкцию в шарнире С на 2 части и рассматривая равновесие каждой части в отдельности можно составить 6 уравнений равновесия (по три для каждого тела), тогда как неизвестных здесь будет семь. 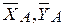 ,MA-для жесткой заделки,
,MA-для жесткой заделки, 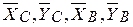 - для шарниров С и В.
- для шарниров С и В.
 |
Рис.5.11.
Причина появления статически неопределимых задач в том, что в теоретической механике мы рассматривали все тела, как абсолютно твердые, недеформируемые. Чтобы эти задачи имели решения, надо учитывать деформации, а тогда появятся дополнительные уравнения и число неизвестных будет равно числу уравнений.
Изучение зависимости между деформациями тел и действующими силами является предметом курса сопротивления материалов, который строится на базе теоретической механики. В этой науке рассматриваются и методы решения статически неопределимых задач.
Вопросы для самоконтроля
1. Запишите и сформулируйте условия равновесия пространственной сходящейся системы сил.
2. Запишите и сформулируйте условия равновесия пространственной параллельной системы сил.
3. Какие формы уравнений равновесия плоской системы сил вы знаете? Какие ограничения при этом накладываются на выбор осей и моментных точек?
4. Какие силы называются сосредоточенными?
5. Какие виды распределенных нагрузок вы знаете?
6. Что такое интенсивность распределенной нагрузки?
7. Какая связь называется жесткой заделкой? Нарисуйте условное обозначение жесткой заделки и изобразите на рисунке ее реакции.
|
|
|
8. Что такое система сочлененных тел? Приведите примеры.
9. В чем заключаются два способа решения задач на равновесие сочлененной системы тел?
10. Какие задачи называются статически определимыми?
11. Какие задачи называются статически неопределимыми? Приведите примеры.
ЗАДАЧИ
1. Жесткая рама в точке А имеет неподвижный опорный шарнир, а в точке В опирается катками на гладкую горизонтальную плоскость. На раму действует пара сил с моментом M=50 кН и сила F=10кН, наклоненная к раме под углом a=300. Необходимые размеры указаны на рис.5.12. Определить реакции опор.
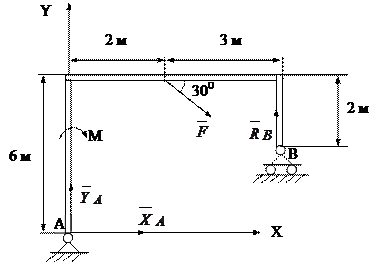 |
Рис.5.12.
Решение: Рассмотрим равновесие рамы. Освободим ее от связей и заменим их действие реакциями связей: 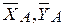 - составляющие реакции неподвижного шарнира в точке А и
- составляющие реакции неподвижного шарнира в точке А и 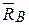 - реакцию катка. Вместе с заданной силой и парой сил они образуют плоскую систему сил. Проведем оси координат и составим уравнения равновесия этой системы:
- реакцию катка. Вместе с заданной силой и парой сил они образуют плоскую систему сил. Проведем оси координат и составим уравнения равновесия этой системы:
åFkx=0 xA+Fcos300=0
åFky=0 yA-Fcos300+RB=0
åmA(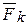 )=0 RB×5-M-F×cos300×6-F×sin300×2==0
)=0 RB×5-M-F×cos300×6-F×sin300×2==0
Отсюда находим:
xA=-F×cos300=-10×0,867=-8,67 кН.
RB= 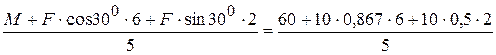 = 24,4 кН
= 24,4 кН
yA=F×cos600-RB=10×0,5-24,4=-19,4 кН.
Отрицательный ответ у силы yA означает, что эта сила должна быть направлена противоположно показанному на чертеже.
2. Найти усилия в стержнях АВ и АС и усилие в тросе AD, если дано, что ÐCBA=ÐBCA=600, ÐEAD=300. Вес груза Р равен 300 Н. Плоскость АВС горизонтальна. Крепления стержней а точках А, В и С шарнирные (рис.5.13).
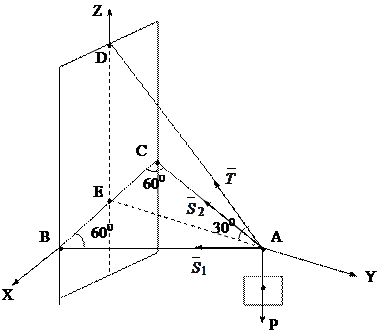 |
Рис.5.13.
Рассмотрим равновесие узла А. На него действует сходящаяся система сил: Р-вес груза, 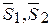 - реакции в стержнях АВ и АС,
- реакции в стержнях АВ и АС, 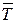 - реакция троса AD.
- реакция троса AD.
Проведем оси координат и составим уравнения равновесия этой системы:
åFkx=0 S1×cos600 - S2×cos600=0
åFky=0 -T×cos300 - S1×cos300-S2×cos300=0
åFkz=0 T×cos600 - P=0
Отсюда T= 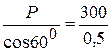 =600 H.
=600 H.
S1=S2=- 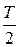 =-300 H.
=-300 H.
3. На трехколесной платформе (рис.5.14) лежит груз весом Р=20 кН. Сила Р приложена в точке D, причем EO=DF=0,1 м и DE=OF=0,5 м. Определить силы давления, производимые колесами на горизонтальную опорную плоскость. Собственным весом платформы пренебречь.
Рассмотрим равновесие платформы. На нее действуют активная сила Р - вес груза и реакции опорной плоскости 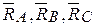 в точках А,В,С. Имеем пространственную систему параллельных сил.
в точках А,В,С. Имеем пространственную систему параллельных сил.
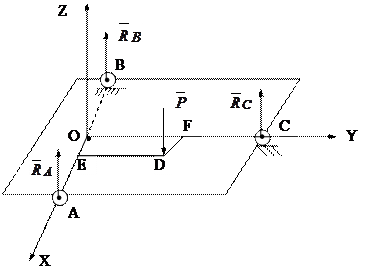
Рис.5.14.
Проведем оси координат и составим уравнения равновесия этой системы сил:
åFkz=0 RA+RB+RC-P=0 (1)
åmx(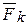 )=0 RC×OC - P×DE=0 (2)
)=0 RC×OC - P×DE=0 (2)
åmy(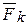 )=0 P×DF - RA ×OA + RB ×OB =0 (3)
)=0 P×DF - RA ×OA + RB ×OB =0 (3)
Из уравнения (2) находим
RC= 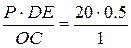 .=10 кн.
.=10 кн.
Подставляя известные числовые значения в уравнения (1) и (3) и перенеся известные члены в правую сторону, получим следующую систему двух уравнений:
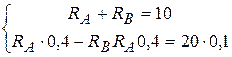
или
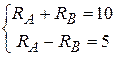
Отсюда RA=7,5 кН, RВ=7,5 кН.
Искомые давления колес на опорную плоскость численно равны найденным реакциям, но направлены в противоположную сторону.
4. Конструкция (рис.5.15) состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг на друга. В точке А конструкция жестко заделана в стену, а в точке В имеет шарнирное крепление. На конструкцию действуют: пара сил с моментом М=60 кН×м, сила F1=10 кН, направленная под углом a=300 к горизонтальной оси и приложенная в точке L, а также горизонтальная сила F2=20 кН, приложенная в точке К. Кроме того на участке ЕН действует равномерно распределенная нагрузка интенсивности q=20 кН/м. Определить реакции связей в точках А,В,С, вызванные этими нагрузками. При окончательных расчетах принять а=0,2 м.
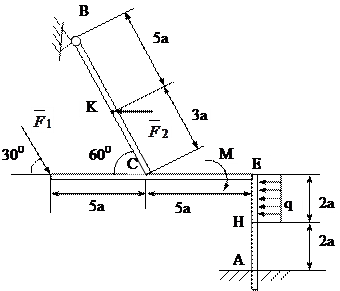 |
Рис.5.15.
Решение: Расчленим конструкцию на две части и рассмотрим равновесие каждой части в отдельности.
а) Стержень ВС. На него действует активная сила 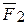 и реакции связей
и реакции связей 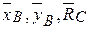 (рис.5.16).
(рис.5.16).
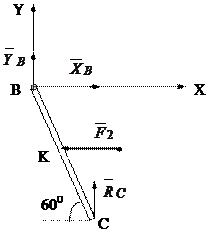 |
Рис.5.16.
Подставим эти уравнения равновесия плоской системы сил:
åFkx=0 xB - F2=0
åFky=0 yB + RC=0
åmB(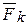 )=0 -F2×5a×sin600 +RC×8a×sin300=0
)=0 -F2×5a×sin600 +RC×8a×sin300=0
Отсюда
xB=+F2=+20 кН
RC =21,68 кН
yB=-RC=-21,68 кН.
б) Угольник AEL (рис.5.17). На него действуют активная сила 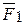 , пара сил с моментом М и равномерно распределенная нагрузка интенсивности q. Освободим угольник от связей и заменим их действие реакциями связей xA, yA, MA,
, пара сил с моментом М и равномерно распределенная нагрузка интенсивности q. Освободим угольник от связей и заменим их действие реакциями связей xA, yA, MA, 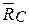 , причем по модулю
, причем по модулю 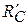 =RC. Равномерно распределенную нагрузку на участке ЕН заменим сосредоточенной силой
=RC. Равномерно распределенную нагрузку на участке ЕН заменим сосредоточенной силой
|
|
|
Q=q×EH= q×2a=20 ×2 ×0,2=8 кН.
Получим уравновешенную плоскую систему сил. Составим три уравнения равновесия:
åFkx=0 xA – Q +F1×cos300 =0
åFky=0 yA – 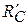 -F1 ×cos600 =0
-F1 ×cos600 =0
åmA(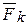 )=0 MA+Q×3a-M+
)=0 MA+Q×3a-M+ 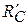 ×5a+F1× cos600 ×10a –F1×cos300×4a =0
×5a+F1× cos600 ×10a –F1×cos300×4a =0
Отсюда
xA=Q- F1 ×cos300 =8-10×0,867=-0,67 кН
yA= 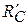 +F1 ×cos600 =21,68+10×0,5=26,68 кН
+F1 ×cos600 =21,68+10×0,5=26,68 кН
MA=-Q×3a+M- 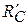 ×5a- F1 ×cos600 ×10a+ F1 ×cos300 ×4a=
×5a- F1 ×cos600 ×10a+ F1 ×cos300 ×4a=
=-8×3×0,2+60-21,68×5×0,2-10×0,5×10×0,2+10×0,867×4×0,2=30,46 кН×м.
 2015-02-27
2015-02-27 16851
16851
