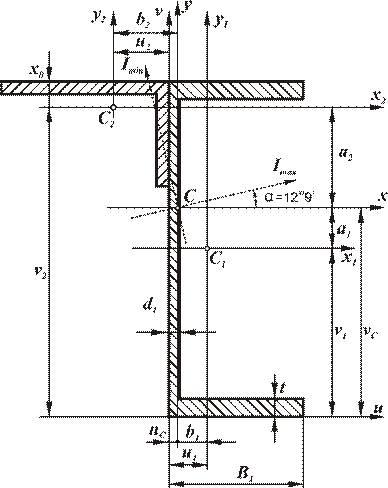
Вычерчиваем сечение в масштабе (рис.), для чего из таблицы сортамента берём следующие данные:
швеллер № 16: 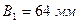 ,
, 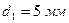 ;
; 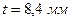 ;
; 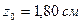 ;
; 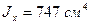 ;
; 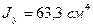 ;
; 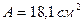 ;
;
уголок 80х50х6: 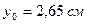 ;
; 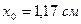 ;
; 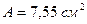 ;
; 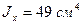 ;
; 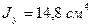 ;
; 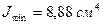
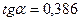 .
.
Показываем положение центров тяжести (точки 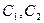 ) каждой фигуры, через которые проводим оси
) каждой фигуры, через которые проводим оси 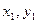 и
и 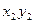 .
.
Следует обратить внимание на то обстоятельство, что положение уголка в заданном сечении не соответствует положе-нию в сортаменте. Поэтому 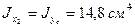 , а
, а 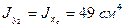 , где
, где 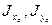 -моменты инерции относительно осей
-моменты инерции относительно осей 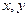 , применяемых в сортаменте.
, применяемых в сортаменте.
Для определения положения центра тяжести сечения выбираем произвольную систему координат 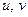 , в которой положение центров тяжести отдельных элементов легко определяется. В данном примере оси проведены по наружному контуру стенки и нижней полки швеллера. Однако можно выбрать любое другое положение осей.
, в которой положение центров тяжести отдельных элементов легко определяется. В данном примере оси проведены по наружному контуру стенки и нижней полки швеллера. Однако можно выбрать любое другое положение осей.
Координаты центра тяжести вычисляем по формулам:
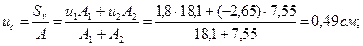
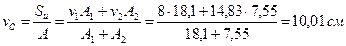 ,
,
где
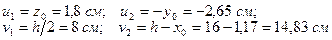
Показываем положение центра тяжести всего сечения – т. 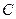 и проводим центральные оси
и проводим центральные оси 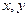 . Cледует подчеркнуть, что для сечения, состоящего из двух фигур, общий центр тяжести располагается на прямой
. Cледует подчеркнуть, что для сечения, состоящего из двух фигур, общий центр тяжести располагается на прямой 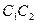 , соединяющей центры тяжести отдельных фигур.
, соединяющей центры тяжести отдельных фигур.
Для вычисления моментов инерции относительно центральных осей 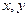 используем зависимость:
используем зависимость:
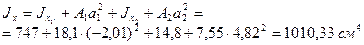 ;
;
здесь
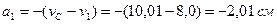 ;
;
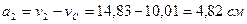 .
.
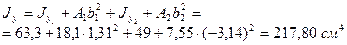 ,
,
здесь
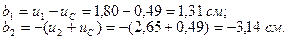
Для определения центробежного момента инерции всего сече-ния 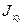 вначале определяем центробежный момент инерции угол-ка относительно собственных центральных осей
вначале определяем центробежный момент инерции угол-ка относительно собственных центральных осей 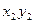 .
.
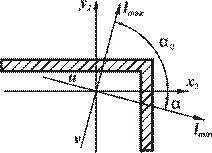
| В сортаменте для уголка 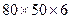 задан задан 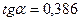 , где , где 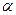 - угол между главной осью - угол между главной осью 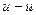 , момент инерции относительно которой равен , момент инерции относительно которой равен 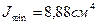 , и осью , и осью 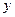 , которая для заданного положения уголка совпадает с осью , которая для заданного положения уголка совпадает с осью 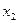 . .
|
| Рис. |
Тогда 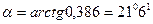 , а угол
, а угол 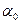 между горизонтальной осью и осью, момент инерции относительно которой равен
между горизонтальной осью и осью, момент инерции относительно которой равен 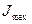 , является дополнительным, то есть
, является дополнительным, то есть 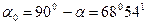 . В данном случае угол
. В данном случае угол 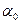 является положительным, так как откладывается против часовой стрелки.
является положительным, так как откладывается против часовой стрелки.
Используя уравнение для заданного по условию задачи положения уголка, можно получить
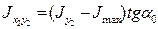 ,
,
а, учитывая, что 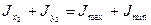 , получаем
, получаем
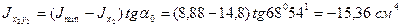 .
.
Центробежный момент инерции всего сечения относи-тельно осей 
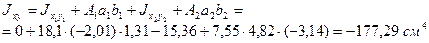
|
| Рис. |
Вычисляем главные моменты инерции
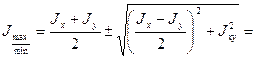
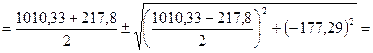
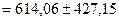 ;
;
Окончательно имеем
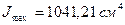 ,
, 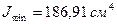
Положение главной оси, относительно которой момент инерции равен 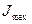 , определим по формуле (2.15)
, определим по формуле (2.15)
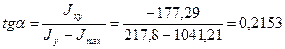
Тогда 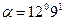 , а так как угол положительный, то на рис. откладываем его против часовой стрелки.
, а так как угол положительный, то на рис. откладываем его против часовой стрелки.
 2015-02-27
2015-02-27 591
591








