Свойства и типы соответствий

Виды соответствий

Соответствие 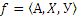называется всюду определенным на множестве X, если:

а) 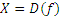, то есть: 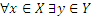: у=f(x), или на «языке» полного образа элемента;

б) 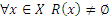, или на «языке» графов;

в) из каждого элемента множества X выходит стрелка и приходит в Y.

Соответствие 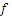называют сюръективным, если:

а) 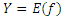, то есть 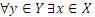: хfу ⇔ у=f(x), или на языке полного прообраза;

б) 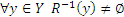, или на «языке» графов;

в) в каждый элемент множества Y приходит стрелка из X.

Если f - всюду определенно на X, то f ^-1 - сюръективное соответствие Y на X, если f - сюрьективно, то f ^-1 всюду определенно на Y.

Соответствие f называют функциональным, если:

а) 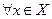R(x) содержит не более одного элемента, то есть ;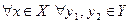
б) на языке графов это означает, что из каждого элемента множества X не выходит две стрелки и более.

Соответствие f называется инъективным, если:

а) 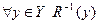содержит неболее одного элемента, то есть ;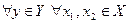

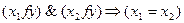б) на «языке» графов это означает, что в каждый элемент множества Y приходит не более одной стрелки.

Из этих определений следует, что соответствие, обратное функциональному, - инъективно, а обратное инъективному - функционально.

Если f и g - всюду определенные, функциональные, инъективные и сюръективные соответствия, то 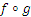- тоже будет обладать всеми этими свойствами.

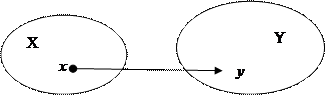
П р и м е р 1: Соответствие на рисунке

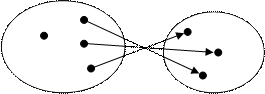а) не всюду определено;

б) функционально;

в) инъективно;

г) сюръективно.

П р и м е р 2: Пусть X - множество студентов в аудитории. Y - множество стульев. Зададим соответствие x f y 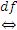«студент x сидит на стуле y».

Это соответствие будет:

а) всюду определенным, если каждый студент будет сидеть;

б) сюрьективным, если все стулья заняты;

в) функциональным, если каждый студент не сидит на двух стульях;

г) инъективным, если на каждом стуле не сидят два студента.

П р и м е р 3: Пусть х f у 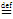(у = sin х), X = R, Y = R. Тогда графиком этого соответствия будет синусоида:

Соответствие это будет:

а) всюду определено, так как 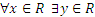: (у = sin х) (любая прямая, параллельная оси ОY, пересекает график функции хотя бы в одной точке).

б) функционально, так как 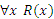состоит из одного элемента (лю­бая прямая, параллельная оси ОУ, пересекает график функции в единственной точке).

в) не инъективно, так как 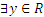, для которых R ^-1(у) состоит более чем из одного элемента (существуют прямые, параллельные оси ОХ, которые пересекают график множество раз).

г) не сюръективно, так как 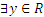, для которых не существует х: у=sinx (существуют прямые, параллельные оси ОХ, которые не пересекают график ни в одной точке).

Рассмотренные выше свойства соответствий (инъективность, сюръективностъ и т.п.) позволяют классифицировать все соответствия на опре­деленные типы. Приведем классификацию соответствий по свойствам в ви­де таблицы:

Функциональность	Всюду определенность	Инъективность	Сюръективность	Название
+				Функция типа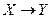
+	+			Отображение из X в Y
+	+	+		Вложение(инъекция) X в Y
+	+		+	Наложение (сюръекция) X на Y
+	+	+	+	Биекция X на Y

Из этой таблицы видно, например, что отображение - это всюду определенное функциональное соответствие.

П р и м е р 4: Отображение 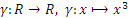сюръективно и инъективно, так как: 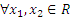из того, что

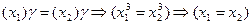
и 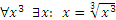. Следовательно, соответствие 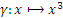- биекция.