Постановка задачи: численно решить линейное дифференциальное уравнение второго порядка
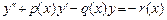 (1)
(1)
с краевыми условиями
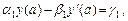 (2)
(2)
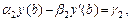 (3)
(3)
где 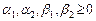 ,
, 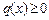 на отрезке
на отрезке 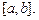 Построить график решения. Для перехода от непрерывной задачи (1)–(3) к дискретной отрезок интегрирования
Построить график решения. Для перехода от непрерывной задачи (1)–(3) к дискретной отрезок интегрирования 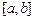 точками
точками 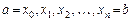 следует разбить на
следует разбить на 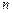 равных частей с постоянным шагом, равным
равных частей с постоянным шагом, равным 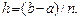 Затем, обозначая
Затем, обозначая 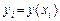 ,
, 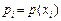 ,
, 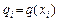 ,
, 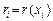 , записать разностный аналог уравнения (1)
, записать разностный аналог уравнения (1)
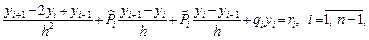 (4)
(4)
где обозначено
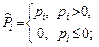
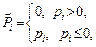
и краевых условий (2)–(3)
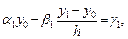 (5)
(5)
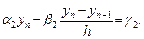 (6)
(6)
Разностное уравнение (4) привести к стандартному трехточечному виду
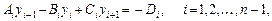
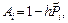
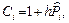 (7)
(7)
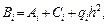
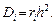
Уравнение (7) с краевыми условиями (5)–(6) решается методом прогонки.
Метод прогонки включает два этапа:
· Прямой ход. Вычисляются прогоночные коэффициенты
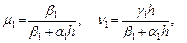
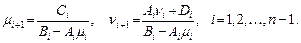
· Обратный ход. Находятся значения неизвестной функции
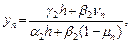
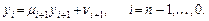
Дополнительные вопросы:
1. Каково условие численной устойчивости метода прогонки?
2. Показать, что метод прогонки является частным случаем метода Гаусса последовательного исключения неизвестных для СЛАУ.
3. Для краевой задачи вида
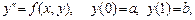
где нелинейная функция 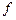 не зависит явно от производной
не зависит явно от производной 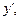 Б. В. Нумеров предложил следующий метод аппроксимации
Б. В. Нумеров предложил следующий метод аппроксимации
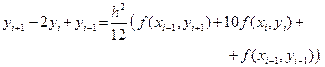 Решить численно этим методом краевую задачу
Решить численно этим методом краевую задачу
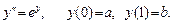
 2015-02-27
2015-02-27 1993
1993
