Решение обыкновеннных дифференциальных уравнений

Постановка задачи: Для обыкновенного дифференциального уравнения

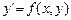(1)

с начальным условием 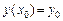, применяя указанные ниже методы, найти с заданной точностью 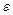приближенное решение на отрезке :

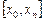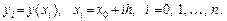
Метод Эйлера с уточнением. За начальное приближение значения функции 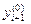на 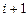-ом шаге берется величина

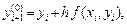(2)

которая затем уточняется по итерационной формуле

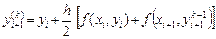(3)

до тех пор не выполнится условие

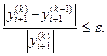(4)

Метод Рунге-Кутты 4-го порядка точности. Решение находится по формулам

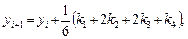
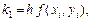
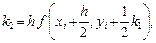(5)

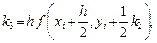
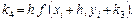
Для достижения заданной точности использовать метод двойного пересчета: по формулам (5) находится 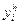при заданном шаге 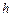и значение 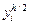, определяемое по тем же формулам при половинном шаге; если не выполняется неравенство

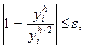(6)

то шаг снова следует уменьшить вдвое и проверить истинность оценки (6) для полученных приближений.

Дополнительные вопросы:

1. Какова точность метода Эйлера с уточнением? Показать, что метод Рунге-Кутты имеет 4-ый порядок точности.

2. Вывести формулы (2), (3), (5) дать их геометрическую интерпретацию. Обосновать оценки (4), (6).

3. Обобщить метод Рунге-Кутты на систему двух обыкновенных дифференциальных уравнений

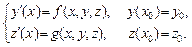
Продемонстрировать решение этим методом на системе уравнений Лотки-Вольтерра «хищник-жертва»

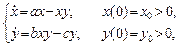
где 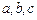— положительные константы, 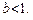Построить графики точного и приближенного решений на фазовой плоскости .

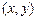4. Исследовать аналитическое и численное решения неустойчивой задачи Коши

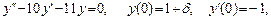
где 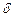— малый параметр. Сравнить решения при значениях 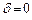и при 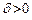. Построить графики решений.