Интерполяция

Постановка задачи: Пусть задана сеточная функция

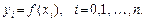(1)

Точки 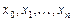называют узлами интерполяции. Требуется найти такую функцию 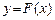, что 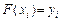для всех 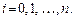Функцию 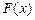называют интерполирующей, она обычно используется, чтобы «доопределить» 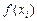на все точки отрезка 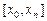. В некоторых случаях считается, что сеточная функция (1) является представлением аналитически заданной функции 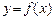, тогда дополнительно ставится вопрос о погрешности интерполяции. В программную реализацию включить графический вывод результатов расчетов. Интерполяцию (1) проводить используя

Многочлен Лагранжа — полином n -ой степени вида

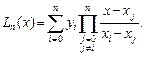(2)

Многочлены Ньютона. Предполагается, что расстояния между узлами интерполяции одинаковы: 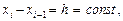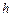— шаг интерполяции. Для интерполирования в начале отрезка используется первая формула Ньютона

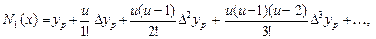
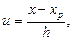
где 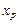— ближайший к 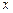слева узел сетки, 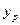— значение сеточной функции в этом узле, 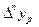— конечная разность p -го порядка.

Для интерполирования в конце отрезка применяется вторая формула Ньютона 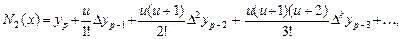где 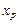— ближайший к 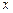справа узел сетки, 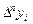— конечная разность n -го порядка, определяемая рекуррентно:

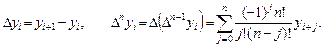
Кубический сплайн — функция, образуемая множеством многочленов 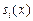степени не выше третьей

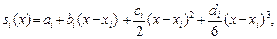(3)

определённых на отрезках 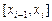, , 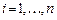так что вся их совокупность 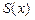составляет дважды непрерывно дифференцируемую на отрезке 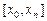функцию и , .

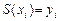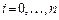Для определения коэффициентов многочленов (3) необходимо вначале методом прогонки (см. лабораторную работу №1.6) решить систему уравнений

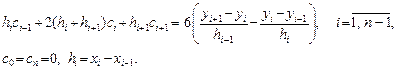Затем найти все другие коэффициенты:

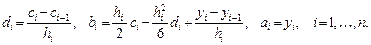
Дополнительные вопросы:

1. Оценить погрешность интерполяции полиномами Лагранжа и Ньютона для функции 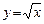в точке 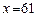на сетке (16,4), (36,6), (49,7), (64,8), (81,9).

2. Вывести все формулы для расчета коэффициентов многочленов (3).