Аппроксимация

Постановка задачи: Пусть задана сеточная функция

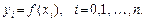(1)

Точки 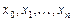называют узлами. Требуется найти (задать аналитически) такую функцию 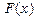, чтобы её уклонение в узлах от соответствующих значений 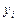было минимальным. В программной реализации следует предусмотреть графический вывод точек 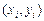и кривой .

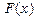Функцию 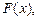называемую аппроксимирующей для сеточной функции (1), выбирать, используя методы:

Метод наименьших квадратов. Аппроксимирующая функция — многочлен степени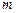

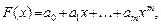(1)

коэффициенты которого определяются из условия минимума суммы квадратов невязок:

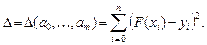
Необходимыми условиями экстремума являются

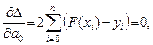
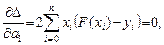
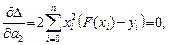(2)

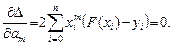
Система (2) — система линейных алгебраических уравнений относительно неизвестных 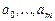вида

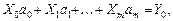
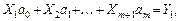(3)

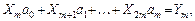
где обозначено

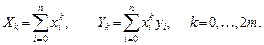
Систему уравнений (3) решить одним из подходящих методов (см. лабораторную работу №1.3).

Аппроксимация кривыми Безье. Пусть количество узлов сетки (1) кратно трём, 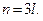Кубические кривые Безье задаются векторным параметрическим уравнением:

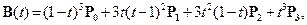(4)

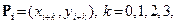
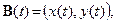
где 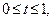и определяются четырьмя точками. Для гладкого сопряжения кривых Безье вначале после каждой третьей точки 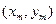исходной сетки (1) вставляется дополнительная точка

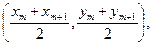
а затем по всем точкам строятся кривые по формуле (4).

Дополнительные вопросы:

1. В чем отличие аппроксимации от интерполяции?

2. Если значения сеточной функции имеют погрешность 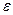, какой точности следует добиваться при аппроксимации по методу наименьших квадратов и как это сделать?

3. Перечислите основные свойства и области применения кривых Безье.