1. Цель работы
Изучение процесса потери устойчивости при осевом сжатии стержня, экспериментальное определение критической силы и сравнение её с теоретическим значением.
2. Основные теоретические положения и методические указания
Одним из наиболее распростаненных видов напряженно-деформированного состояния в судостроении и судоремонте является продольное сжатие стержней. Так, например, при работе двигателя внутреннего сгорания шатун в каждом рабочем цикле при сгорании топлива испытывает такую сжимающую нагрузку. В условиях продольного сжатия работают стрелы судовых кранов и ряд других элементов СТС.
Отличительной особенностью разрушения таких элементов является внезапная потеря устойчивости, заключающееся в потере формы элемента при определенном уровне силового воздействия. При этом при меньших нагрузках оно практически незаметно.
Такое воздействие вызывается критической силой – наименьшей осевой сжимающей силой, способной удержать в равновесии слегка искривленный сжатый стержень.
Устойчивым называют такое равновесное состояние деформированного тела, когда при любом малом отклонении от этого состояния тело стремится возвратиться к нему после устранения причин, вызвавших это отклонение. В этом случае во время нагружения действовали только упругие напряжения и деформации.
Если же тело после устранения этих причин займет новое равновесное состояние (останется пластически деформированным), то говорят о потере устойчивости и его первоначальное состояние называют неустойчивым.
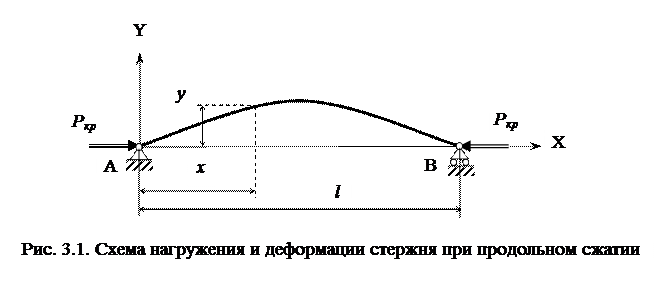
Устойчивость формы равновесия зависит от величины приложенных к телу нагрузок. Нагрузку, превышение которой вызывает потерю устойчивости, называют критической. Для прямолинейного стержня, сжатого продольной силой P, в упругой стадии деформирования для наиболее опасной наименьшей критической силы справедлива формула Эйлера
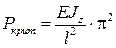
где Е – модуль продольной упругости материала стержня (модуль Юнга);
l –длина стержня;
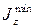 – минимальное значение момента инерции поперечного сечения стержня;
– минимальное значение момента инерции поперечного сечения стержня;
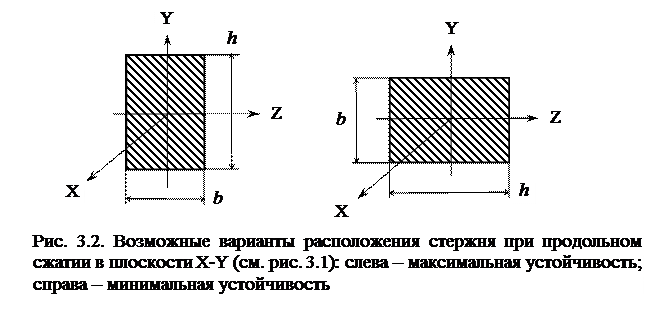
Численное значение критической силы зависит не только от формы и размеров сечения стержня, но и от его положения (рис. 3.2).
В сопротивлении стержней продольному изгибу основную роль играет гибкость стержня, определяемая с учетом величины наименьшего радиуса инерции стержная является важнейшей характеристикой для определения его устойчивости.
3. Оборудование, инструмент и образцы,
необходимые для выполнения работы
Для исследования потери устойчивости при осевом сжатии и определения критической силы взят стержень 1 из полосовой стали. Опыт проводится на специальной установке, общий вид которой и схема показаны на рисунке 3.3.
Установка состоит из станины 2(рис. 3.3)и рычага 3 с шарнирной опорой 4, с помощью которого через бобышку передается осевое усилие на стержень 1 от груза 7. Стержень своими ножевыми окончаниями устанавливается на опоры 5 и 6 строго в вертикальной плоскости и в результате реализуется шарнирное его опирание с обеих сторон (μ = 1).

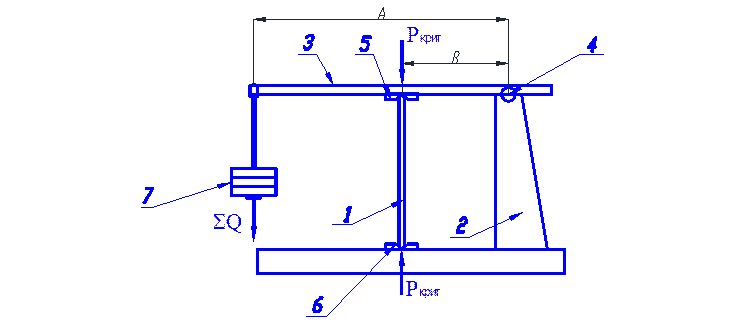 Рис. 3.3. Установка для исследования устойчивости стержня прямоугольного сечения. Общий вид установки (вверху) и ее принципиальная схема (внизу)
Рис. 3.3. Установка для исследования устойчивости стержня прямоугольного сечения. Общий вид установки (вверху) и ее принципиальная схема (внизу)
4. Порядок и методика выполнения работы
· Провести обмеры размеров стержня, занести в таблицу наблюдений его длину, ширину и толщину.
· Произвести нагружение укладыванием грузов весом 10 Н на подвеску 8 (рис. 3. 1); при каждом новом нагружении проверять стержень на потерю устойчивости. Для этого легким нажимом руки примерно в середине пролёта в направлении меньшего размера сечения стержень отклоняется всвоей плоскости от положения равновесия и затем отпускается.
· Если стержень после ряда колебаний около равновесного положения вернется к первоначальной форме, то его состояние отвечает устойчивой формой равновесия и критическое значение нагрузки еще не достигнуто.
· По достижении определенного значения суммарной нагрузки 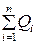 стержень, будучи отклоненным в своей плоскости от положения равновесия, останется в отклоненном состоянии, отвечающем состоянию "безразличного равновесия", которое и соответствует критическому значению силы
стержень, будучи отклоненным в своей плоскости от положения равновесия, останется в отклоненном состоянии, отвечающем состоянию "безразличного равновесия", которое и соответствует критическому значению силы 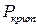 .
.
· Определим численное значение критической силы 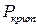 с учетом длины рычагов подвески груза и расположения испытуемого образца:
с учетом длины рычагов подвески груза и расположения испытуемого образца:
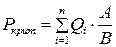 , Н
, Н
· С целью установления возможности определениякритической силы по формуле Эйлера найти минимальный радиус инерции сечения стержня и его гибкость 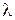 :
:
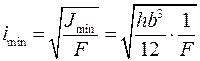 ;
; 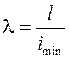
· Сравнивая полученное значение с общепринятой предельной гибкостью для малоуглеродистой стали λпред = 100, выясняют правомочность использования формулы Эйлера.
· Закончить оформление отчета и представить его преподавателю для защиты.
5. Контрольные вопросы.
· Дать определение устойчивости элемента.
· Какое равновесие называют устойчивым?
· Что понимают под неустойчивым равновесием?
· Что называют критической силой?
· Привести схему нагружения и деформации стержня при продольном сжатии (изгибе).
· Привести формулу для определения критической силы.
3. Определение деформаций консольных элементов
корпуса судна при изгибе
1. Цель работы
Определение экспериментальным путем величин прогибов и углов поворота некоторых сечений балки и сравнение полученных величин перемещений с их теоретическими значениями.
2. Основные теоретические положения и методические указания
Современное судно представляет собою сложную инженерную конструкцию, в которой важную роль играют консольные элементы – несущие строительные конструкции, жестко закрепленные одним концом при свободном другом или части конструкции, выступающие за опору. Типичным представителем консольных элементом являются крылья ходового мостика судна, консольные краны и др.
В большинстве случаев консольным элементам (балкам)[2] приходится работать в режиме "плоский поперечный изгиб под действием сосредоточенной силы" (рис. 3.1.), результатом которого являются деформации.
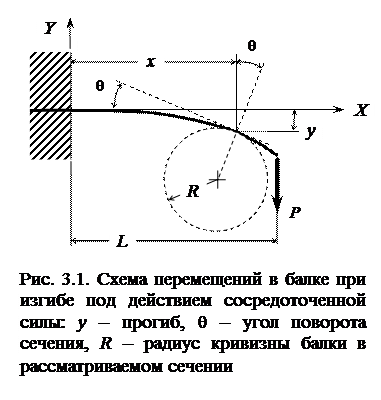 Для простейшего случая изгиба — плоского изгиба балок, при котором все заданные нагрузки действуют в одной, т.н. силовой плос- кости, они проявляется в:
Для простейшего случая изгиба — плоского изгиба балок, при котором все заданные нагрузки действуют в одной, т.н. силовой плос- кости, они проявляется в:
· потере прямолинейности и появлении кривизны оси R (x);
· повороте поперечных сече-ний балки на угол θ(x);
· появлении прогиба балки у (х).
Предельно-допустимые значения этих элементов деформации обычно задаются при разработке конструкции, а затем (например, во время ходовых испытаний судна) измеряются и сопоставляются с заданными величинами с целью проверки соблюдения условий его жесткости:
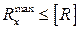 ;
; 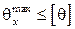 ;
; 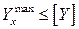 .
.
В основу расчетов деформации балок положены математические зависимости кривизны плоской кривой 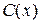 , с одной стороны — от 2-ой производной уравнения изогнутой оси балки, с другой стороны — от величины изгибающего момента в рассматриваемом сечении
, с одной стороны — от 2-ой производной уравнения изогнутой оси балки, с другой стороны — от величины изгибающего момента в рассматриваемом сечении 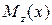 :
:
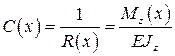
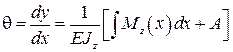
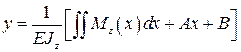
Полученные значения прогибов и углов поворота сравнивают с допустимыми, значения которых обычно не превышают следующих величин:
§ прогиб — не более 0,001 …0,004 длины пролета;
§ угол поворота сечения — не более 0,25 … 0,5 °.
Теоретический расчет линейных и угловых перемещений сечений балки производится по указанию преподавателя, и может быть проведен методом начальных параметров или методом единичной силы (формула Мора, правило Верещагина). В простейших случаях нагружения балок возможно использование справочных данных.
Для сравнения величин линейных и угловых перемещений, полученных в опытах и расчетным путем, подсчитывается расхождение между ними 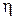 в процентах к расчетным значениям.
в процентах к расчетным значениям.
3. Оборудование и инструмент,
необходимые для выполнения работы
Общий вид и схема лабораторной установки приведены на рис. 3. 2 (вверху и внизу соответственно).
 |
На плите 1 стендового стола с помощью болтовых соединений 2 устанавливается стойка 3, в которой закрепляется балка прямоугольного поперечного сечения 4. Нагружение осуществляется грузами 5, которые устанавливаются на подвесах 6 и имеют возможность перемещения вдоль балки. Вертикальные перемещения точек балки измеряют индикаторами 7 часового типа.
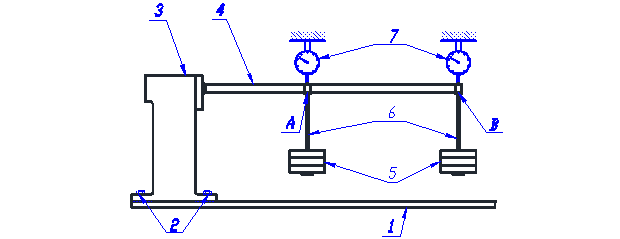 Рис. 3.2. Общий вид лабораторной установки (вверху)
Рис. 3.2. Общий вид лабораторной установки (вверху)
и ее принципиальная схема (внизу)
Точки измерения (А) и расположения груза задаются преподавателем. Измерения элементов деформации консольного элемента производят индикатором часового типа И-50 с точностью 0,01 мм.
Масса грузов определяется с помощью электронных весов с точностью не ниже 5 г.
4. Порядок и методика выполнения работы
· В указанных точках (А и В) сечения балки (рис. 3.2) расположить подвесы для грузов и установить индикаторы.
· Установить стрелки индикаторов на "нуль".
· Произвести предварительное нагружение; разгрузить балку и проверить положение стрелок индикатора (возврат их в исходное положение).
· Нагрузить балку в точке А силой 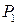 и зафиксировать показания индикатора в этой же точке (DА1).
и зафиксировать показания индикатора в этой же точке (DА1).
· Затем в точке В нагрузить балку силой 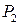 , измерить перемещение в точке 2 (DВ2) и перемещение в точке 1.
, измерить перемещение в точке 2 (DВ2) и перемещение в точке 1.
· Разгрузить балку. Стрелки индикаторов должны вернуться в нулевое положение.
· Произвести нагружение в обратном порядке: сначала нагрузить балку силой 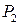 в точке А и снять показание индикатора в этой точке (DА2). Затем – силой
в точке А и снять показание индикатора в этой точке (DА2). Затем – силой 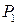 и замерить перемещения в точке В (DВ1).
и замерить перемещения в точке В (DВ1).
· Разгрузить балку. Проверить упругость материала балки - возвращение индикаторов на ноль.
· Зная эти перемещения и длину тяги r, устанавливают величину тангенса угла 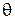 (рис.1); с учетом малых деформаций рассчитывают угла поворота сечения
(рис.1); с учетом малых деформаций рассчитывают угла поворота сечения 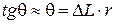 .
.
· Записать результаты опыта в таблицу, сопоставить экспериментальные и теоретические данные, сделать необходимые вычисления.
· Закончить оформление отчета и представить его преподавателю для защиты.
5. Контрольные вопросы.
· Дайте определение консольного элемента
· В каком режиме приходится работать консольному элементу?. Приведите формулу для определения угла поворота сечения консольной балки:
· Приведите значения предельно допустимых углов поворота сечения и величины прогиба консольной балки
4. Определение силовой характеристики
винтовой пружины сжатия
1. Цель работы
Построение силовой характеристики пружины, определение её жёсткости и сравнение полученных результатов с теоретическими.
2. Основные теоретические положения и методические указания
В механизмах современных машин, станков, аппаратов и приборов важную роль играют различные упругие элементы и, прежде всего – пружины. Обеспечивая своей упругостью необходимое натяжение или нажатие, аккумулируя энергию или действуя как амортизатор, пружины являются ответственным звеном. Особенно широко используются витые пружины.
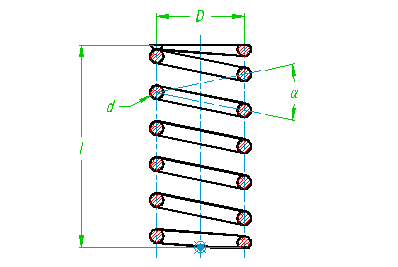
Рис. 4.1
Исходная геометрия цилиндрической пружины определяется следующими параметрами:
· D - диаметр образующего цилиндра или средний диаметр пружины;
· a - угол подъёма винтовой линии;
· l - длина оси рабочей части пружины;
· n - число рабочих витков пружины;
· d - диаметр проволоки, свитой в пружину.
При сжатии винтовой цилиндрической пружины в любом поперечном сечении витка возникают крутящий и изгибающий моменты, поперечная и нормальная силы.
Однако при малом угле подъёма винтовой оси проволоки напряжения и перемещения, обусловленные изгибающим моментом, нормальной и поперечной силами, малы. Поэтому при определении напряжений и перемещений в цилиндрических пружинах растяжения и сжатия учитывают только действие крутящего момента. Так, осевое удлинение пружины при растяжении силой Р можно определить с помощью интеграла Мора
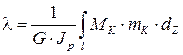
где MK и mK - грузовой и единичный крутящие моменты в поперечном сечении проволоки, свитой в пружину, вызванные, соответственно, силой Р и безразмерной силой Р = 1; GJP - жёсткость проволоки на кручение; JP - полярный момент инерции поперечного сечения круглой проволоки
JP» 0,1p d 4; G - модуль сдвига материала пружины; n – число витков пружины.
Полагая cos a» 1 (ввиду малости a) и учитывая, что полная длина рабочей части пружины l = p × D× n, можно получить зависимость изменения высоты пружины от осевой силы P:
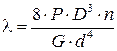
4. Порядок и методика выполнения работы
Для выполнения работы используется приспособление, собранное на базе разрывной машины УММ-5 (см. рис. 1. 3).
·  Испытываемая пружина 1 (рис. 4.2.) закрепляется в траверсах 2 и 3, реакция на перемещение подвижной траверсы фиксируется динамометром машины УММ-5. Для предотвращения выпадения пружины из траверсы при приложении нагрузки используется страховочный стержень 4.
Испытываемая пружина 1 (рис. 4.2.) закрепляется в траверсах 2 и 3, реакция на перемещение подвижной траверсы фиксируется динамометром машины УММ-5. Для предотвращения выпадения пружины из траверсы при приложении нагрузки используется страховочный стержень 4.
· Подвергнуть пружину предварительному сжатию и зафиксировать точку, определяющую исходное положение пружины и соответствующую ему силу Р 0.
· Занести в таблицу исходные данные.
· Последовательно сжимать пружину, перемещая подвижную траверсу машины на фиксированные расстояния, замерять силу сжатия для каждого единичного перемещения.
· Занести в таблицу данные наблюдений, построить силовую характеристику пружины: l - f (Р).
· По полученным данным определить экспериментальную жёсткость пружины как силы, вызывающей её единичное удлинение: 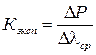 , Н/м
, Н/м
· Учитывая, что модуль сдвига пружинной стали G = 0,8·105 МПа, и используя исходные данные: диаметр пружины D, число ее витков n, диаметр проволоки d, найти теоретическую жесткость пружины: 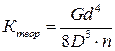
· Определить относительную погрешность эксперимента: 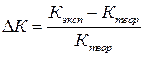 .
.
· Закончить оформление отчета и представить его преподавателю для защиты.
5. Контрольные вопросы.
· Что понимают под силовой характеристикой пружины?
· Перечислите известные Вам типы пружин
· Перечислите нагрузки и напряжения, возникающие в пружине при сжатии
· Перечислите основные геометрические характеристики витой пружины сжатия
· Приведите формулу для определения изменения длины пружины при ее сжатии
 2015-02-27
2015-02-27 909
909








