1. Угол между двумя прямыми в пространстве.
Возьмем в пространстве две непараллельные прямые 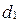 и
и 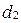 . Тогда
. Тогда 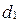 и
и 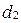 являются либо пересекающимися, либо скрещивающимися. Если
являются либо пересекающимися, либо скрещивающимися. Если 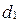 и
и 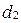 пересекаются, то они образуют четыре угла. Тогда углом между
пересекаются, то они образуют четыре угла. Тогда углом между 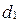 и
и 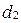 называется тот из четырех углов, который по величине не превосходит остальные.
называется тот из четырех углов, который по величине не превосходит остальные.
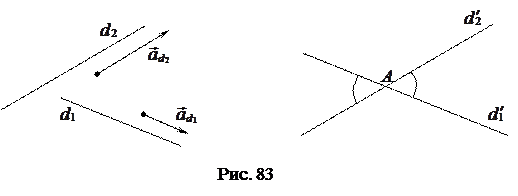 Пусть
Пусть 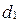 и
и 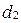 являются скрещивающимися. Возьмем в пространстве произвольную точку
являются скрещивающимися. Возьмем в пространстве произвольную точку 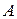 и проведем через нее прямые
и проведем через нее прямые 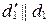 и
и 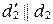 (рис. 83). Прямые
(рис. 83). Прямые 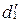 и
и 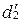 образуют четыре угла с вершиной
образуют четыре угла с вершиной 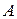 . Тот из них, который по величине не превосходит остальные, называется углом между прямыми
. Тот из них, который по величине не превосходит остальные, называется углом между прямыми 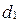 и
и 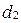 .
.
Выведем формулу для вычисления косинуса угла между прямыми 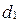 и
и 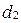 . Пусть
. Пусть 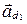 и
и 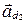 - направляющие векторы прямых
- направляющие векторы прямых 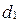 и
и 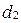 соответственно. Возможны два случая:
соответственно. Возможны два случая:
а) Если 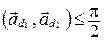 , то
, то 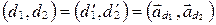 . Тогда
. Тогда 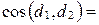
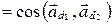 .
.
б) Если 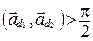 , то
, то 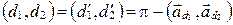 . Тогда
. Тогда 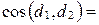
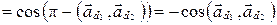 .
.
Из пунктов а), б) следует, что 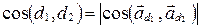 . Таким образом,
. Таким образом,
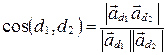 . (35)
. (35)
2. Условие перпендикулярности двух прямых в пространстве.
Из формулы (35) получаем:
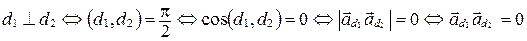 .
.
Итак,
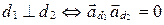
(две прямые в пространстве взаимно перпендикулярны тогда и только тогда, когда скалярное произведение их направляющих векторов равно нулю).
Заметим, что взаимно перпендикулярные прямые в пространстве могут быть как пересекающимися, так и скрещивающимися.
3. Угол между прямой и плоскостью.
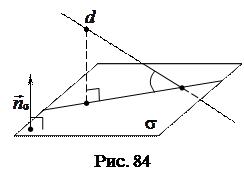 Напомним, что прямая называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.
Напомним, что прямая называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.
Если  не перпендикулярна
не перпендикулярна 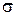 , то углом между прямой
, то углом между прямой  и плоскостью
и плоскостью 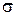 называется острый угол между прямой
называется острый угол между прямой  и ее проекцией на плоскость
и ее проекцией на плоскость 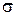 (рис. 84).
(рис. 84).
Если 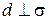 , то угол между
, то угол между  и
и 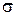 считается равным
считается равным 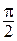 .
.
Пусть 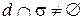 и
и  не перпендикулярна
не перпендикулярна 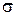 ,
, 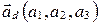 - направляющий вектор прямой
- направляющий вектор прямой  , а плоскость
, а плоскость 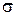 задана в прямоугольной декартовой системе координат общим уравнением
задана в прямоугольной декартовой системе координат общим уравнением 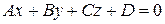 . Найдем величину угла
. Найдем величину угла 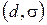 между прямой
между прямой  и плоскостью
и плоскостью 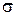 . Положим
. Положим 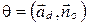 .
.
Возможны два случая:
а) Если 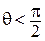 (рис. 85, а), то
(рис. 85, а), то 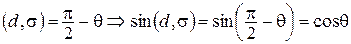 .
.
б) Если 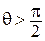 (рис. 85, б), то
(рис. 85, б), то
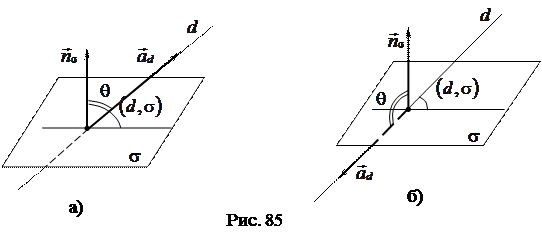
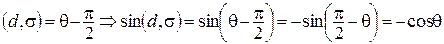 .
.
Из пунктов а), б) следует, что 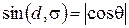 . Учитывая, что
. Учитывая, что 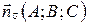 , получаем:
, получаем:
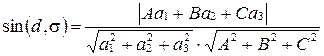 . (36)
. (36)
Заметим, что если 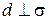 , то
, то 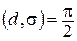 , тогда
, тогда 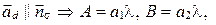
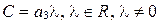 (соответственные координаты коллинеарных векторов пропорциональны). Тогда левая часть формулы (36) будет равна:
(соответственные координаты коллинеарных векторов пропорциональны). Тогда левая часть формулы (36) будет равна:
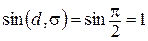 ,
,
а правая – 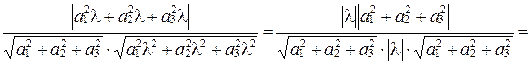
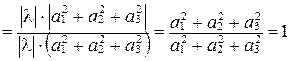 .
.
Таким образом, если 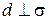 , то формула (36) также справедлива.
, то формула (36) также справедлива.
4. Условие перпендикулярности прямой и плоскости.
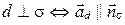 . Применяя условие коллинеарности двух векторов в координатах, получим:
. Применяя условие коллинеарности двух векторов в координатах, получим:
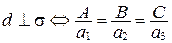 .
.
 2015-02-27
2015-02-27 378
378








