· Формула де Бройля, выражает связь длины волны 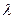 с импульсом р движущейся частицы, для двух случаев:
с импульсом р движущейся частицы, для двух случаев:
а). в нерелятивистском случае (p = m 0 V), если V << c
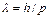 ; (3.6)
; (3.6)
б). в релятивистском случае (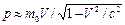 ), если V → c,
), если V → c,
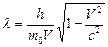 , (3.7)
, (3.7)
где: h – постоянная Планка;
m 0 – масса покоя частицы;
V – скорость частицы;
с – скорость света в вакууме.
· Связь длины волны де Бройля с кинетической энергией Т частицы
а) для нерелятивистского случая
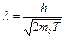 ; (3.8)
; (3.8)
б) для релятивистского случая
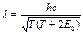 , (3.9)
, (3.9)
где Е 0= m 0 с – энергия покоя.
· Соотношения неопределенностей Гейзенберга имеют вид
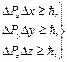 (3.10)
(3.10)
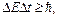 (3.11)
(3.11)
где D Px – неопределенность проекций импульса на ось х;
Δ E – неопределенность энергии частицы;
Δ t – неопределенность времени;
Δ x – неопределенность координаты.
· Если потенциальное поле U не зависит от времени, то можно записать стационарные уравнения Шредингера. Для одномерного случая уравнения будут иметь вид:
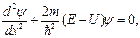 (3.12)
(3.12)
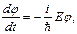 (3.13)
(3.13)
где Е – энергия частицы;
ψ – функция, зависящая от х;
φ – функция, зависящая от t.
Волновая функция частицы
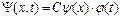 (3.14)
(3.14)
определяется решениями (3.12) и (3.13).
· Для свободного электрона выражение (3.14) прнимает плоской волны, движущейся в направлении х:
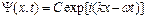 , (3.15)
, (3.15)
где kx - ωt – фаза волны.
· Участок волны, имеющий данное значение фазы и движущийся в вдоль оси х имеет фазовую скорость:
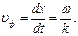 (3.16)
(3.16)
· В реальном случае волны де Бройля накладываются друг на друга, образуя волновой пакет, который движется с групповой скоростью υr:
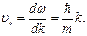 (3.17)
(3.17)
Эта скорость совпадает со скоростью распространения частицы.
· Вероятность dW обнаружить частицу в интервале dx (для одномерного случая) выражается формулой:
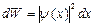 . (3.18)
. (3.18)
Вероятность W обнаружить частицу в интервале от x 1 до x 2 находится интегрированием:
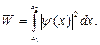 (3.19)
(3.19)
Собственное значение энергии En частицы, находящейся на n- ом энергетическом уровне в бесконечно глубокой потенциальной яме, выражается формулой:
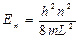 ,
, 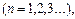 (3.20)
(3.20)
где L – ширина потенциальной ямы.
Собственная волновая функция, соответствующая (3.20) имеет вид:
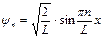 . (3.21)
. (3.21)
· Коэффициент преломления n волн де Бройля на границе потенциальной ступени, если 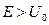 (низкая потенциальная ступень) имеет вид:
(низкая потенциальная ступень) имеет вид:
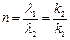 . (3.22)
. (3.22)
Коэффициенты отражения R и прохождения А волн де Бройля через низкую потенциальную ступень (рис. 3.2):
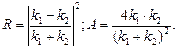 (3.23)
(3.23)
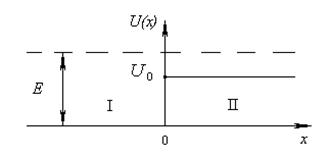
Рис. 3.2
· Коэффициент прозрачности D прямоугольного потенциального барьера ширины d (рис. 3.3)
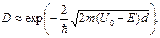 (3.24)
(3.24)
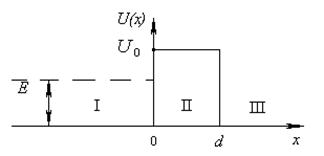
Рис. 3.3
· Собственное значение энергии электрона в водородоподобном атоме:
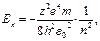 (3.25)
(3.25)
где n – главное квантовое число (n=1,2,3,...);
ε0 – электрическая постоянная;
z –число протонов в ядре атома.
· Квантовый гармонический осциллятор имеет энергию:
Еп = hν (n +1/2), (3.26)
где n – квантовое число.
· Энергия фонона также определяется формулой
Еф = hν. (3.27)
 2015-02-27
2015-02-27 4370
4370
