Примеры решения задач

Пример 1. Определить температуру, при которой в проводнике вероятность найти электрон с энергией 0,5 эВ над уровнем Ферми равна 2%.

Решение: Система подчиняется распределению Ферми-Дирака (3.31). В это выражение подставляем исходные данные:

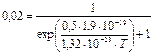
Проведя необходимые вычисления, получим:

Т = 1490К.

Пример 2. Плотность металла γ = 8,9?10³ кг/м³, молярная масса М = 63,5, валентность – 1. Найти концентрацию электронного газа и энергию Ферми (Т = 0).

Решение: Определим концентрацию носителей заряда:

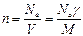
Энергия Ферми определим из соотношения (3.36):

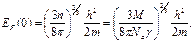
Подставляя необходимые данные и проведя расчеты, получим искомые результаты:

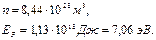
Пример 3. Определить концентрацию носителей заряда в чистом германии при Т = 300К. На сколько градусов нужно повысить температуру от начальной (300К), чтобы число электронов проводимости в германии увеличилось в двое.

Решение: Используя выражение для концентрации носителей (3.39), найдем отношение концентраций электронов:

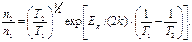
Учитывая, что степенная функция температуры значительно слабее экспоненциальной, можно записать:

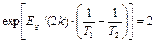
Подставляя исходные данные и проведя необходимые вычисления, получим:

Т ₂=317К.

Т.е. необходимо увеличить температуру на 17К.

Пример 4. Определить положение уровня Ферми в германии п- типа при Т = 300К, если на 2·10⁶ атомов германия приходится один атом примеси. Концентрация атомов в германии равна 4,4·10²⁸ м^-3. Предэкспоненциальный множитель , , .

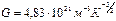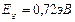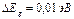Решение: Концентрация свободных электронов определяется из условий:

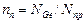
где N_пр – концентрация примеси.

Для величины концентрации основных носителей справедливо известное соотношение:

.

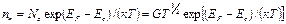Можно записать выражение:

.

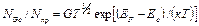После логарифмирования равенства получим:

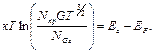
Подставляя исходные данные и проведя необходимые вычисления, получим:

,

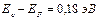следовательно, уровень Ферми находится на 0,18 эВ ниже дна зоны проводимости.

Пример 5. Найти положение уровня Ферми относительно середины запрещенной зоны при Т = 300 К для кристалла германия, содержащего 5·10¹⁶ см^-3 атомов мышьяка.

Решение: Воспользуемся формулой, полученной в примере 4.

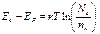
Считаем, что 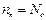т.е. все примесные атомы однократно ионизированы.

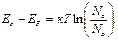
Подставляя исходные данные и проведя необходимые вычисления, получим:

.

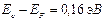Поскольку ширина запретной зоны германия 0,66 эВ, то уровень Ферми находится на 0,17 эВ выше середины запрещенной зоны.

Пример 6. Удельное сопротивление собственного германия при Т = 300К составляет 0,43 Ом·м Подвижности электронов и дырок равны соответственно 0,39 и 0,19 м²/(В·с). Определите собственную концентрацию электронов и дырок.

Решение.

Удельная проводимость полупроводника σ определяется из уравнения

σ =1/ ρ = n_ie (μ_p + μ_n).

Отсюда

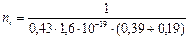= 2,5·10¹⁹ м⁻³.

Пример 7. Образец германия легирован примесью атомов сурьмы так, что 1 атом примеси приходиться на 2·10⁶ атомов германия (N). Предполагается, что все атомы примеси ионизированы при 300 К и концентрация атомов германия N_Ge  = 4,4·10²⁸ м⁻³. Определить концентрацию электронов, дырок, удельное сопротивление материала, коэффициенты диффузии электронов и дырок.

Решение.

Определим концентрацию донорных примесей

N _д  = N _Ge/ N = 2,2·10²² м⁻³.

Собственная концентрация носителей была определена и равна 2,5·10¹⁹ м⁻³, можно найти концентрацию дырок

.

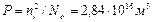Удельное сопротивление легированного полупроводника можно определить как .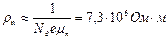

Определим коэффициенты диффузии электронов и дырок в германии при Т=300К с помощью соотношения Эйнштейна D = kTμ / e.

D_n  = kTμ_n / e = 10.0 · 10^-3 м²/с

D_p  = kTμ_p /e = 4,9 · 10^-3 м²/с

Пример 8. В электронном германиевом полупроводнике длиной l = 1 м один конец нагрет и существует распределение концентрации носителей

n (x) =  n:(x ²+2 x +1)

Какова скорость изменения концентрации носителей в его центре, если напряжение на его концах U = 1 В.

Решение. Запишем уравнение непрерывности (3.48) в виде

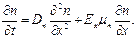
Найдем производные и напряженность поля:

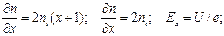
Запишем уравнение

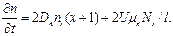
Подставив справочные данные (см. приложение), получим

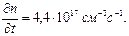
Пример 9. Определить ток, протекающий через тонкую пленку, если известно, что этот ток ограничен пространственным зарядом, площадь контакта S = 1 мм², толщина пленки d = 1·10^-8 м, μ_n  = 20 см²/Вс, ε = 3,8, U = 10 мВ.

Решение. Используем формулу (3.50):

I ≈ g / bεε ₀ μ_nSU ²/ d ³

Подставим необходимые данные, проведем вычисления и получим ответ

I = 72 мкА.

Задачи

3.1. Какова вероятность заполнения электронами уровней расположенных на kT; 2 kT; 3 kT выше и ниже уровня Ферми.

3.2. На каком расстоянии (в единицах kT) от уровня Ферми находятся уровни, вероятность заполнения которых 0,1 и 0.9.

3.3. Вычислить среднюю энергию свободных электронов в металлическом натрии при Т = 0 К. Известно, что 1 м³ натрия содержит 2,53·10²⁸ атомов.

3.4. Определить концентрацию n свободных электронов в металле при Т = 0К. Энергия Ферми 1 эВ.

3.5. Определить отношение концентраций свободных электронов при Т = 0К в литии и цезии, если известно, что уровни Ферми в этих металлах соответственно равны 4,72 эВ и 1,53 эВ.

3.6. Вычислить среднюю кинетическую энергию электронов в металле при Т = 0 К если уровень Ферми 7 эВ

3.7. Определить отношение концентрации n _max электронов в металле (Т = 0 К), энергия которых отличается от максимальной не более чем на Δ E_k концентрации n _min электронов, энергии которых не превышают значения E =? E;? E принять равным 0,01 E_F

3.8. Определить максимальную скорость V _max электронов в металле при Т = 0К, если E_F =5 эВ

3.9. Металл находиться при температуре Т = 0 К. Определить во сколько раз число электронов со скоростями 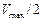до 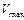больше числа электронов со скоростями от 0 до V _max/2.

3.10. Определить уровень Ферми E_F в собственном полупроводнике, если энергия активации равна 0,1 эВ. За нулевой уровень отсчета кинетической энергии электронов принять дно зоны проводимости.

3.11. Определить концентрацию свободных носителей заряда в чистом кремнии при Т = 300 К.

3.12. Во сколько раз изменится концентрация собственных носителей заряда в кремнии при увеличении его температуры с 300 до 400 К?

3.13. Найти положение уровня Ферми в собственном полупроводнике относительно средины запрещенной зоны при Т = 300 К, если эффективная масса электрона в два раза больше эффективной массы дырки.

3.14. В чистом полупроводнике при Т = 300 К концентрация собственных носителей составляет 1,5·10¹⁶ м^-3 эффективные массы электронов проводимости и дырок одинаковы. Определить E_F.

3.15. При какой температуре концентрация собственных носителей в кремнии будет равна концентрации собственных носителей в германии при Т = 300К.

3.16. Какова вероятность найти электрон на дне зоны проводимости в собственном германии (E_q = 0,72 эВ), если температура образца равна: а). 30 К; б). 300 К; в). температура плавления 937ºС?

3.17. Какова вероятность найти электрон на дне зоны проводимости при Т = 300 К; а). в собственном германии (E_g  = 0,72 эВ); б). собственном кремнии (E_g  = 1,12 эВ); в). в алмазе(E_g  = 5,6 эВ)? Что означают эти результаты?

3.18. Уровень Ферми полупроводника находиться на 0,3 эВ ниже дна зоны проводимости. Какова вероятность того, что при комнатной температуре энергетические уровни, расположенные на расстоянии 3 kT выше дна зоны проводимости, заняты электронами? Какова вероятность того, что потолок валентной зоны, содержит дырки, если
E_g  = 1,1 эВ.

3.19. Вычислить положение уровня Ферми относительно дна зоны проводимости при Т = 400 К для кристалла германия содержащего 5·10¹⁶ атомов сурьмы в 1 см³

3.20. Удельная проводимость кремния примесями равна 112 См/м. Определить подвижность дырок и их концентрацию, если постоянная Холла 3,66·10^-4 м³/Кл. Принять, что полупроводник обладает только дырочной проводимостью.

3.21. Определить удельное электрическое сопротивление кремния при температуре 300 К если концентрация донорной примеси равна 10²⁰ м^-3. Подвижность электронов в кремнии при 300 К принять равной
0,14 м²/(В·с).

3.22. Концентрация носителей в кремнии равна 5·10¹⁰ см^-3, подвижность электронов μ_n  = 0,15 м²/(В·с) и дырок μ_p  = 0,05 м²/(В·с). Определить сопротивление кремниего стержня длинной 5 см и сечением 2 мм².

3.23. Определить удельное электрическое сопротивление кремния p-типа при температуре 300 К, если концентрация акцепторной примеси 20 м^-3. Подвижность дырок при температуре 300 К принять равной 0,05 м²/(В·с)

3.24. Образец германия содержит примесь фосфора 2·10²⁰ м^-3. Определить а). удельное сопротивление и тип проводимости при 300К; б). концентрацию германия необходимую для изменения типа проводимости, чтобы удельное сопротивление стало равным 0,006 Ом·м; в). процент содержания примеси в этом образце. Принять μ_n  = 0,39 м²/(В·с); μ_p  = 0,19 м²/(В·с) при Т = 300К.

3.25. Определить удельную электропроводимость кремния при Т = 300К, если N_a  = 2,3·10¹⁹ м³; N_д  = 2,2·10¹⁹м^-3.

3.26. Ток j = 10³A/м² течет через кристалл германия n-типа с ρ = 0,05 Ом·м. За какое время электроны пройдут расстояние 5·10^-5 м?

3.27. Образец кремния p-типа длинной 5 м, шириной 2 мм, толщиной 1 мм и имеет сопротивление 100 Ом. Определить концентрацию примеси и отношение электронной проводимости к дырочной. Принять n_i  = 2,5·10¹⁶м^-3; μ_n  = 0,12 м²/(В·с); μ_p = 0,025 м²/(В·с) Т = 300К.

3.28. Термистор из собственного кремния имеет сопротивление 600 Ом при 300К. Вычислить его сопротивление пи 325К, предполагая, что ширина запрещенной зоны кремния 1,1 эВ и что подвижности носителей μ_n и μ_p не изменяются в этом интервале температур.

3.29. Коэффициент Холла образца примесного кремния равен 3,66·10^-4 м³/Кл, удельное сопротивление образца ρ = 993·10³ Ом·м. Определить концентрацию и подвижность носителей заряда, предполагая, что заряды одного знака.

3.30. Определить относительное положение уровня Ферми в кремниевом полупроводнике p-типа и концентрацию неосновных носителей заряда, если концентрация акцепторной примеси 10¹⁶ см^-3, а Т = 300К.

3.31. В кристалле германия n-типа на каждые 10⁸ атомов германия приходиться один атом донорной примеси. Полагая, что эффективная масса электрона 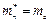, найти положение уровня Ферми относительно дна зона проводимости (Т=300К)

3.32. В кристалле кремния p-типа на каждые 10⁸ атомов кремния приходиться один атом акцепторной примеси. Найти положение уровня Ферми при комнатной температуре относительно валентной зоны.

3.33. Определить концентрацию электронов и дырок при Т = 300К: а). в собственном кремниевом полупроводнике; б). в кристалле кремния, содержащим 5·10¹⁷ атомов сурьмы в 1 см³.

3.34. Определите: а). удельное сопротивление собственного германия при Т = 300К; б). чему будет равно удельное сопротивление, если к этому образцу добавить донорную примесь так чтобы один атом донорной примеси приходился на каждые 10⁸ атомов германия?

3.35. Определить: а). удельное сопротивление собственного кремния при Т = 300К; б). каково будет удельное сопротивление этого кремния, если к этому образцу добавить донорную примесь так, чтобы один атом донорной примеси приходился на каждые 10⁸ атомов германия?

3.36. Образец собственного кремния имеет удельное сопротивление 2000 Ом·м при комнатной температуре и концентрации электронов проводимости n_i  = 1,4·10¹⁶ м^-3. Определить удельное сопротивление образца, легированного акцепторной примесью с концентрацией 10²¹ и 10²³ м^-3. Предположите, что подвижность остается одинаковой как для собственного так и для примесного кремния и равной μ_p  = 0,25 μ_n.

3.37. Определить концентрацию неосновных носителей заряда, их подвижность в образце германиевого полупроводника p-типа, если концентрация акцепторной примеси 10^-16 см^-3, а коэффициент диффузии электронов D_n  = 93 см²/с (Т=300К).

3.38. Определить удельную проводимость образца кремния при Т=300К, если концентрация акцепторов в полупроводнике N_a  = 2,3·10¹³ см^-3

3.39. Покажите, что полупроводник имеет минимальную удельную проводимость при данной температуре, когда концентрация электронов 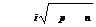. Чему равна концентрация дырок в этих условиях?

3.40. Изменение удельной проводимости германия показало, что она изменяется с температурой по закону exp (-4350/ Т). Требуется определить ширину запрещенной зоны германия.

3.41. Определить среднюю скорость дрейфа электронов и дырок в германии при 300К, если к образцу приложено электрическое поле с напряженностью E = 10, 100 и 1000 В/см.

3.42. Решить предыдущую задачу для кремния.

3.43. Определите длину диффузионного смещения электрона при Т = 300К в кристалле германия n-типа, если подвижность электронов 3900 см²/(В·с), а время их жизни τ_n  = 100 мкс.

3.44. Образец дырочного антимонида индия имеет подвижность электронов 6,2 м²/(В·с) при Т = 290К. Вычислить диффузионную длину неосновных носителей заряда, если их время жизни τ = 3 ·10^-8с.

3.45. Коэффициент Холла образца примесного кремния равен 9,93·10^-4 м³/Кл, удельное сопротивление образца ρ = 9,93·10³ Ом·м. Определить концентрацию и подвижность носителей заряда, предполагая, что эти носители одного знака.

3.46. Образец полупроводника имеет коэффициент Холла
R_н  = 3,66·10^-4 м³/Кл и удельное сопротивление ρ = 8,93·10^-3 Ом·м. Для обнаружения эффекта Холла образец помещается в магнитное поле с индукцией B = 0,5 Тл. Определить угол Холла.

3.47. Образец полупроводника 30 мм´5 мм´1 мм имеет сопротивление 500 Ом. При помещении его в магнитное поле В = 0,5 Тл, перпендикулярное плоскости пластины. На гранях образца возникает ЭДС Холла U_Н  = 5 мB при токе через образец 10 мА. Определить подвижность Холла и плотность носителей в полупроводнике, считая, что он p-типа. До какого значения изменится ЭДС Холла, если в то же поле поместить образец меди таких же размеров и несущий такой же то n_си  = 8,5·10²⁸ м^-3.

3.48. Образец германия n-типа имеет удельное сопротивление
ρ = 1,5 Ом·см; R_н  = 5,4·10³ см³/Кл. Определить концентрацию основных носителей заряда и подвижность.

3.49. Удельное сопротивление легированного кристалла кремния ρ = 9,27·10³ Ом·м и R_н  = 3,8·10⁴ м³/Кл. Найти концентрацию и подвижность носителей, если имеется только один тип носителей.

3.50. Коэффициент Холла образца примесного кремния равен 3,66·10^-4 м³/Кл, удельное сопротивление образца ρ = 9,93·10³ Ом·м. Определить концентрацию и подвижность носителей заряда, если заряды одного знака.

3.51. Оценить факторы, влияющие на величину слагаемых уравнения непрерывности.

3.52. Проанализировать возможные варианты уравнения непрерывности.

3.53. Оценить ток в полупроводнике, пользуясь уравнением непрерывности.

3.54. Через тонкую диэлектрическую пленку течет ток надбарьерной инжекции. Оценить его величину, если Т = 300К, Ф ₀ = 2 эВ, S = 1 мм².

3.55. Рассчитать ток, ограниченный пространственным зарядом через тонкую диэлектрическую пленку, если ε = 5, μ_n  = 2 см²/вс, d = 10^-8 м,
U = 20 мВ.