Этот способ применяется, когда точка движется по заданной линии (траектории). Уравнением 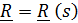 задается линия, по которой движется точка; закон движения по ней
задается линия, по которой движется точка; закон движения по ней 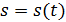 , где
, где 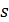 – дуговая координата, т. е. длина дуги со знаком.
– дуговая координата, т. е. длина дуги со знаком.
Базисные векторы 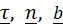 , называемые натуральным триэдром, вводятся следующим образом (рис.3.1,в):
, называемые натуральным триэдром, вводятся следующим образом (рис.3.1,в):
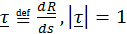 – единичный вектор (орт) касательной,
– единичный вектор (орт) касательной,
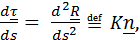 где
где 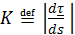 – кривизна,
– кривизна, 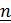 – орт главной нормали,
– орт главной нормали,
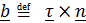 – единичный вектор бинормали.
– единичный вектор бинормали.
Векторы 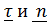 лежат в так называемой соприкасающейся плоскости – предельном при
лежат в так называемой соприкасающейся плоскости – предельном при 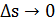 положении плоскости, содержащей
положении плоскости, содержащей 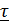 (s) и
(s) и 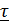 (s+
(s+  . Кривизна
. Кривизна 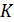 характеризует скорость изменения направления касательной; обратную ей величину
характеризует скорость изменения направления касательной; обратную ей величину 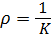 называют радиусом кривизны траектории.
называют радиусом кривизны траектории.
Вектор скорости
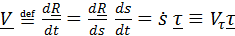 , (3.6)
, (3.6)
где 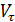 является проекцией (единственной) вектора скорости на направление касательной и может быть любого знака.
является проекцией (единственной) вектора скорости на направление касательной и может быть любого знака.
Дифференцируя еще раз, получаем вектор ускорения  .
.
Производную 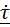 запишем как производную сложной функции:
запишем как производную сложной функции:
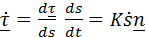 , тогда
, тогда
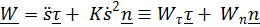 , (3.7)
, (3.7)
где 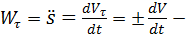 касательное (тангенциальное) ускорение,
касательное (тангенциальное) ускорение,
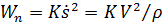 – нормальное ускорение.
– нормальное ускорение.
«Кинематический» подход часто используется дпя вычисления кривизны траектории при координатном способе задания движения. Вычисляется скорость  и ее значение
и ее значение 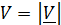 ; ускорение
; ускорение  и его значение
и его значение 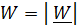 ; касательное ускорение
; касательное ускорение 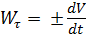 , (либо
, (либо 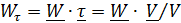 ); нормальное ускорение
); нормальное ускорение 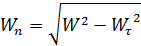 и радиус кривизны
и радиус кривизны 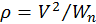 .
.
 2015-02-04
2015-02-04 500
500








