Воздействия (силы и моменты) характеризуются главным вектором сил 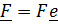 и главным моментом
и главным моментом 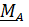 относительно произвольной опорной точки. Запишем формулу, связывающую моменты относительно двух точек – опорной точки
относительно произвольной опорной точки. Запишем формулу, связывающую моменты относительно двух точек – опорной точки 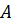 и так называемой точки приведения
и так называемой точки приведения 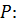
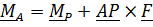 . (2.9)
. (2.9)
Если есть такая точка приведения 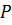 , относительно которой главный момент
, относительно которой главный момент 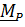 равен нулю, то говорят, что система приводится к равнодействующей, приложенной в точке приведения. Из формулы(2.9)
равен нулю, то говорят, что система приводится к равнодействующей, приложенной в точке приведения. Из формулы(2.9) 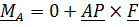 следует,что приведение к равнодействующей возможно, только если главный момент
следует,что приведение к равнодействующей возможно, только если главный момент 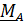 и главный вектор
и главный вектор 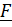 перпендикулярны. При этом множество точек приведения к равнодействующей находятся на прямой, уравнение которой найдем, умножив векторно формулу
перпендикулярны. При этом множество точек приведения к равнодействующей находятся на прямой, уравнение которой найдем, умножив векторно формулу 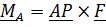 на вектор
на вектор 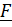 (рис. 2.8a):
(рис. 2.8a):
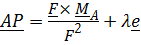 , (2.10)
, (2.10)
где 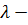 произвольный параметр.
произвольный параметр.
Рассмотрим систему параллельных сил 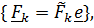 где
где 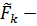 проекция
проекция 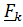 на направление, задаваемое ортом
на направление, задаваемое ортом 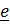 . Главный вектор
. Главный вектор 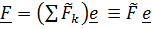 и главный момент
и главный момент 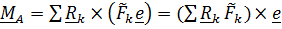 перпендикулярны, поэтому система приводится к равнодействующей.
перпендикулярны, поэтому система приводится к равнодействующей.
| dz |
| R |
| z |
| Рис. 2.8. Центр параллельных сил (а) и центр тяжести (б) |
| A |
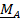
|
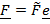
|
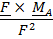
|
| ⦁ P |
| а) |
| б) |
Покажем, что в этом случае на прямой (2.10) существует такая точка приведения
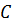 , называемая центром параллельных сил, положение которой не
, называемая центром параллельных сил, положение которой не
изменяется при повороте всех сил на произвольный угол (точки приложения сил не изменяются).
Подставляя выражения 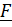 и
и 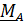 в (2.10) и раскрывая двойное векторное произведение, получим
в (2.10) и раскрывая двойное векторное произведение, получим
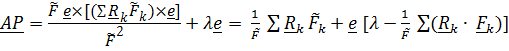 .
.
Чтобы это выражение не зависело от направления сил (вектора 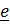 ), надо принять
), надо принять 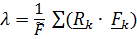 и вектор положения центра параллельных сил:
и вектор положения центра параллельных сил:
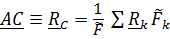 .(2.11)
.(2.11)
Частный случай параллельных сил – силы тяжести, действующие на точки тела. Если тело небольшого размера, то можно пренебречь различием в направлении сил (к центру Земли) и различиями в величине сил ввиду разного расстояния до центра Земли. Тогда центр тяжести совпадает с центром масс
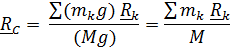
Оценим различие в положениях центра масс и центра тяжести «высокого» тела, например, небоскреба (рис 2.8,б). Обозначим 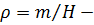 линейная плотность массы. Сила тяжести, действующая на элемент массы
линейная плотность массы. Сила тяжести, действующая на элемент массы 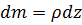 равна
равна 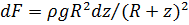 , где
, где 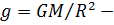 ускорение на поверхности Земли.
ускорение на поверхности Земли.
Суммарная сила тяжести 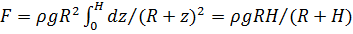 ; координата центра тяжести
; координата центра тяжести 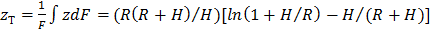 . Заменяя
. Заменяя 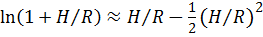 , получим
, получим 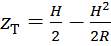 . Для высоты
. Для высоты 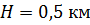 получим, что центр тяжести ниже центра масс всего на
получим, что центр тяжести ниже центра масс всего на 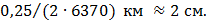
 2015-02-04
2015-02-04 642
642








