Глава 3. Кинематика точки

Положение точки в системе отсчета задается вектором положения 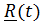как функцией времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A.

Траекторией называется кривая, по которой движется точка, скоростью 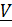– производная по времени вектора положения 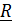, ускорением 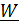– производная от вектора скорости:

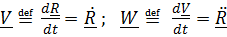. (3.1)

Из определения производной вектора следует, что вектор скорости направлен по касательной к траектории. Собственно говоря, формулами (3.1) вся кинематика точки и исчерпывается; все технические трудности связаны лишь с выбором системы координат.

Упражнение 3.1. Исходя из определения производной вектор – функции от скалярного аргумента

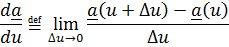
показать, что

1) 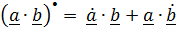(производная скалярного произведения);

2) 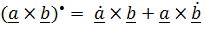(производная векторного произведения);

3) Если 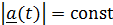, то 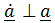(производная вектора постоянной длины перпендикулярна этому вектору).