Каноническое уравнение эллипса:
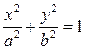 . (14)
. (14)
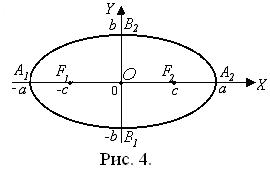 Термины и обозначения основных элементов эллипса (рис. 4):
Термины и обозначения основных элементов эллипса (рис. 4):
O – центр эллипса;
с – фокусное расстояние;
F 1(– c; 0), F 2(c; 0) – фокусы эллипса;
| А1А2 | = 2 a – длина большой оси;
а – большая полуось эллипса;
| B1B2 | = 2 b – длина малой оси;
b – малая полуось эллипса.
Для эллипса справедливо: c 2 = a 2– b 2.
Число 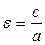 называется эксцентриситетом эллипса
называется эксцентриситетом эллипса 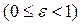 .
.
Если a < b, то эллипс имеет вытянутую по вертикали форму (рис. 5).
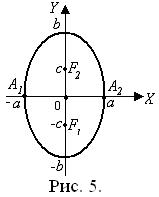 В этом случае фокусы эллипса F 1(0; – c), F 2(0; c), эксцентриситет
В этом случае фокусы эллипса F 1(0; – c), F 2(0; c), эксцентриситет 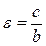 и справедливо c 2 = b 2 – a 2.
и справедливо c 2 = b 2 – a 2.
Если a = b, то уравнение эллипса становится уравнением окружности:
x 2 + y 2 = R 2 ,
где R= a= b.
В этом случае фокусы эллипса совпадают с центром окружности, фокусное расстояние с = 0, эксцентриситет окружности 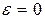 .
.
Каноническое уравнение гиперболы:
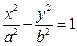 . (15)
. (15)
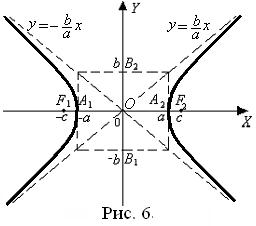 Термины и обозначения основных элементов гиперболы (рис. 6):
Термины и обозначения основных элементов гиперболы (рис. 6):
O – центр гиперболы;
с – фокусное расстояние;
F1 (– c; 0), F2 (c; 0) – фокусы гиперболы;
| А1А2 | = 2 a – длина вещественной оси;
а – вещественная полуось гиперболы;
| B1B2 | = 2 b – длина мнимой оси;
b – мнимая полуось гиперболы.
Уравнения асимптот гиперболы:
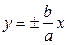 .
.
Для гиперболы справедливо: с 2 = a 2 + b 2.
Число 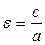 называется эксцентриситетом гиперболы
называется эксцентриситетом гиперболы 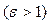 .
.
Канонические уравнения параболы.
Существуют 4 вида канонических уравнений параболы:
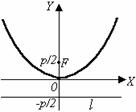 | х 2 = 2 ру. (16) Фокус F (0; 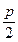 ), уравнение директрисы: у = – ), уравнение директрисы: у = – 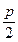 . . |
| Рис. 7. | |
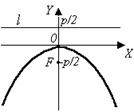 | х 2 = –2 ру. (17) Фокус F (0; – 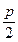 ), уравнение директрисы: у = ), уравнение директрисы: у = 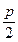 . . |
| Рис. 8. | |
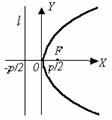 | у 2 = 2 рх. (18) Фокус F (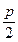 ; 0), уравнение директрисы: х = – ; 0), уравнение директрисы: х = – 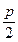 . . |
| Рис. 9. | |
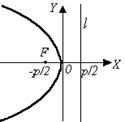 | у 2 = –2 рх. (19) Фокус F (– 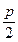 ; 0), уравнение директрисы: х = ; 0), уравнение директрисы: х = 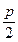 . . |
| Рис. 10. |
Термины и обозначения основных элементов параболы: O – вершина параболы, F – фокус параболы, p – параметр параболы (расстояние от фокуса F до директрисы l).
Для приведения уравнения кривой со смещенным центром к каноническому виду может быть использован параллельный перенос системы координат ХОY в точку O 1(α; β). При параллельном переносе координаты любой точки М (х; у) в новой системе координат X 1 O 1 Y 1 будут (х 1; у 1), где
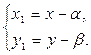 (20)
(20)
Примеры таких преобразований приведены в таблице 2.
Таблица 2.
| В системе координат ХОY | В системе координат X 1 O 1 Y 1 |
Окружность с центром в точке O 1(α; β) и с радиусом R: 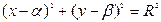 | Каноническое уравнение окружности: 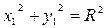 |
Эллипс с центром в точке O 1(α; β): 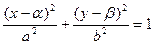 | Каноническое уравнение эллипса: 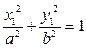 |
Гипербола с центром в точке O 1(α; β): 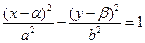 | Каноническое уравнение гиперболы: 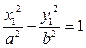 . . |
Параболы с вершиной в точке O 1(α; β) 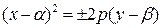 или или 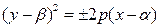 . . | Канонические уравнения парабол: 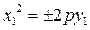 или или 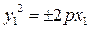 |
 2015-02-04
2015-02-04 1384
1384
