2015-02-27
522
Используя формулы (2) и (3) и, предполагая верным утверждение о преобразовании Фурье от произведения функций, получаем:
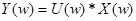, где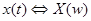 
, откуда вытекает
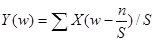(4)
Эта формула устанавливает связь между непрерывным и дискретным преобразованиями Фурье. Как и следовало ожидать,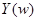 
имеет период 
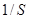, что согласуется с (1).
Предположим, что спектр исходного сигнала ограничен: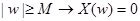 
для некоторого 
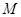. Выберем 
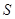таким образом, чтобы выполнялось неравенство
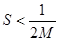(5)
В этом случае функция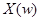 
однозначно определяется функцией 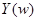. Значение 
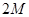называется частотой выборки Найквиста. Если частота выборки больше указанной величины, спектр непрерывного сигнала может быть восстановлен по спектру дискретного. Позже будет показано, что и сам непрерывный сигнал восстанавливается по дискретному.
