П.9. Применение степенных рядов для вычисления функций и определенных интегралов

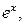
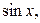
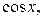
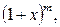
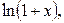
Для вычисления значения функции при данном значении аргумента можно воспользоваться разложением этой функции в степенной ряд. В частности, удобно воспользоваться приведенными в предыдущем пункте разложениями в ряд Маклорена функций 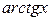. Если значение аргумента 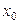принадлежит области сходимости, то после разложения функции в ряд и подстановки 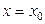искомое значение функции представляет собой сумму числового ряда. Поскольку полную сумму ряда, представляющую собой точное значение функции, найти, как правило, затруднительно, то в этом ряде сохраняется такое количество первых членов, которое гарантирует необходимую в данном конкретном случае точность. Точность вычислений задается обычно одной значащей цифрой в каком-либо разряде. Так, запись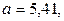 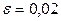означает, что точное значение величины 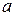находится в пределах от 5,39 до 5,43. Это можно записать следующим образом: 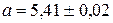. Другими словами, заданная точность 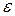- это та погрешность, в пределах которой приближенное значение может отличаться от точного.

Для приближенного вычисления определенного интеграла нужно разложить в степенной ряд подынтегральную функцию, проинтегрировать степенной ряд почленно и сохранить в ряде достаточное для обеспечения заданной точности количество его первых членов; при этом область интегрирования не должна выходить за рамки области сходимости ряда.