2015-02-04
642
Степенным рядом называется функциональный ряд вида
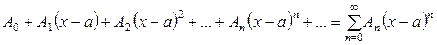, (14)
где a, A0, A1, A2, …, An, … - действительные числа.Частный случай степенного ряда при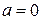 
:
.
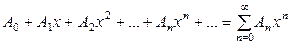Теорема Абеля. Если степенной ряд (14) сходится при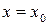 
, то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству
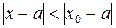. (15)
Если же ряд (14) расходится при 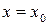, то он расходится и при любом x, удовлетворяющем неравенству
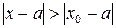. (16)
Поясним формулировку теоремы Абеля. После несложных преобразований условия (15) и (16) можно соответственно записать в виде
,
.
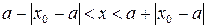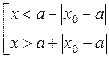Отсюда следует, что число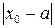 
в окрестности точки a образует симметричный относительно нее интервал. При этом если ряд сходится при 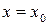, то гарантирована его сходимость и внутри интервала. Если же он расходится при 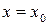, то он обязательно расходится и во всех точках вне интервала. Таким образом, теорема Абеля фактически устанавливает существование симметричного относительно точки 
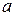интервала абсолютной сходимости степенного ряда. Половина его длины обозначается R и называется радиусом сходимости, а точка 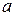- центром сходимости.
Радиус сходимости R может принимать значения от 0 до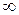 
, т.е. 
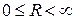. Интервал абсолютной сходимости может быть записан в виде 
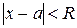. Сходимость ряда в точках 
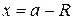и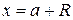 
должна быть исследована особо, и в случае ее установления соответствующая граница добавляется к интервалу, образуя область сходимости.
Применив к степенному ряду признак сходимости Даламбера, для радиуса сходимости можно получить формулу
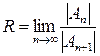. (17)
Эта формула справедлива только в тех случаях, когда ряд содержит все целые степени разности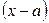 
, т.е. не имеет нулевых коэффициентов.
Если же для анализа сходимости степенного ряда применить радикальный признак Коши, то получится формула
.
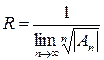Теорема. Любой степенной ряд внутри его интервала сходимости можно почленно интегрировать и дифференцировать; при этом его радиус сходимости сохраняется, а сумма ряда также интегрируется или дифференцируется.
