2015-02-04
514
Функциональный ряд вида
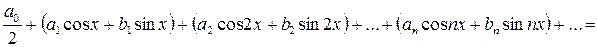
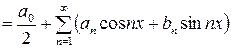(19)
называется тригонометрическим рядом.
Если коэффициенты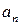 
и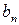 
вычислены по формулам
, 
, 
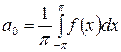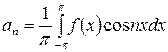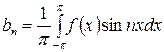, (20)
то тригонометрический ряд (19) представляет собой ряд Фурье для функции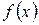 
, заданной на отрезке 
.
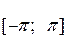Теорема Дирихле. Если 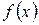- кусочно гладкая на отрезке 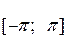функция, то ее ряд Фурье сходится к функции 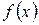во всех точках, где она непрерывна. В точках разрыва 
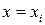ряд сходится к значению 
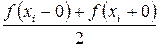, а на концах интервала – к значению 
.
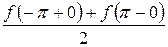В силу теоремы Дирихле для функции, заданной на отрезке 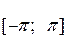и для периодической функции с периодом 
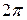в точках непрерывности справедливо равенство:
,
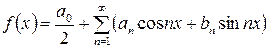где коэффициенты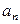 
и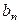 
вычисляются по формулам (20).
Для четной функции, заданной на отрезке 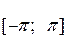или для четной с периодом с периодом 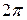коэффициенты 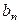при нечетных членах ряда Фурье оказываются нулевыми, и ряд принимает вид
,
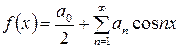где
; 
.
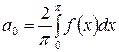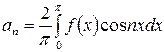Аналогично для нечетных функций:
; 
.
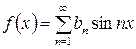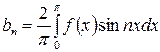Ряд Фурье для функции, заданной на отрезке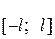 
и для периодической функции с периодом 
:
,
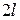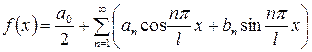где
, 
, 
.
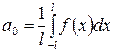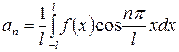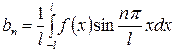Здесь для четных функций:
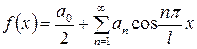, где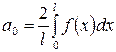 
, 
;
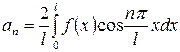для нечетных функций:
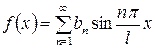, где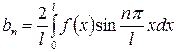 
.
Если требуется представить рядом Фурье функцию, заданную на отрезке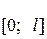 
, то ее формально можно доопределить четным или нечетным образом в промежутке 
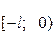и применить приведенные выше формулы.
