Рядом Тейлора для функции 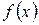 называется степенной ряд
называется степенной ряд
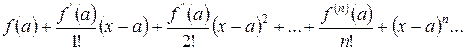 . . | (18) |
При этом говорят, что ряд Тейлора построен для 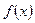 в точке
в точке 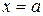 .
.
Остаток ряда Тейлора может быть записан в форме Лагранжа:
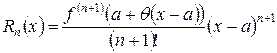 , , 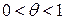 . . |
Если функция 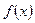 бесконечно дифференцируема в некоторой области
бесконечно дифференцируема в некоторой области 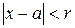 и при этом в этой области выполняется условие
и при этом в этой области выполняется условие
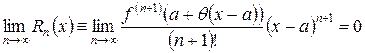 , ,  |
то ряд (17) в данной области сходится к функции 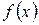 , т.е. справедливо равенство
, т.е. справедливо равенство
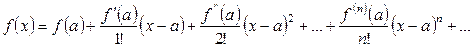 . . |
Частный случай ряда Тейлора при 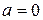 называется рядом Маклорена. Остаток ряда Маклорена в форме Лагранжа имеет вид:
называется рядом Маклорена. Остаток ряда Маклорена в форме Лагранжа имеет вид:
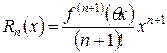 , , 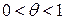 , , |
а разложение функции в ряд Маклорена, при условии 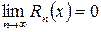 , выглядит следующим образом:
, выглядит следующим образом:
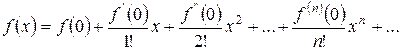 . . |
Если 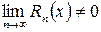 , то ряд Тейлора (Маклорена), даже если он сходится, имеет сумму, отличную от
, то ряд Тейлора (Маклорена), даже если он сходится, имеет сумму, отличную от 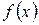 .
.
Ряды Маклорена для некоторых элементарных функций, представленные ниже вместе с их областями сходимости, полезно запомнить для их применения при разложении других, более сложных функций.
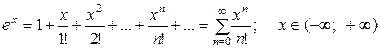 .
.
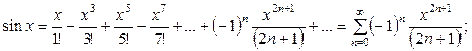
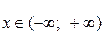 .
.
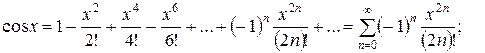
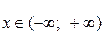 .
.
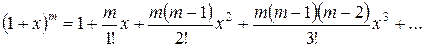
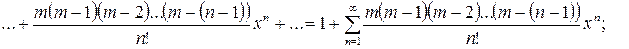
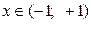 .
.
Последний ряд называется биномиальным, т.к. функция, для которой построен этот ряд, представляет собой бином (двучлен) произвольной степени 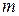 . Гарантированная область сходимости биномиального ряда указана для любых значений
. Гарантированная область сходимости биномиального ряда указана для любых значений 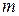 ; для некоторых значений она может быть расширена в ту или другую сторону (или в обе) включением в нее границы интервала.
; для некоторых значений она может быть расширена в ту или другую сторону (или в обе) включением в нее границы интервала.
Частные случаи биномиального ряда выглядят следующим образом:
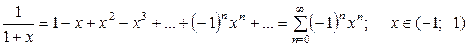 .
.
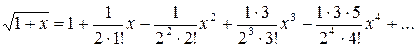
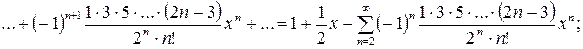
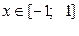 .
.
Из первого частного случая могут быть получены ряды еще для двух часто встречающихся в практических задачах функций:
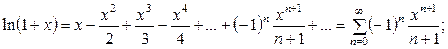
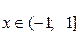 ;
;
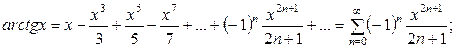
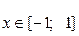 .
.
 2015-02-04
2015-02-04 1452
1452
