Определение 2. Функция f (x) называется кусочно-непрерывной на сегменте [ a, b ], если она непрерывна во всех точках сегмента [ a, b ] за исключением, быть может, конечного числа точек, в которых она имеет разрыв первого рода.
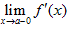
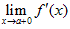 Определение 3. Кусочно-непрерывная на сегменте [ a, b ] функция называется кусочно-гладкой на этом сегменте, если производная этой функции f ' (x) существует и непрерывна всюду на сегменте [ a, b ], за исключением, быть может, конечного числа точек, в которых существует правый и левый пределы и.
Определение 3. Кусочно-непрерывная на сегменте [ a, b ] функция называется кусочно-гладкой на этом сегменте, если производная этой функции f ' (x) существует и непрерывна всюду на сегменте [ a, b ], за исключением, быть может, конечного числа точек, в которых существует правый и левый пределы и.
Лемма 1. Об аппроксимации непрерывной на сегменте [ a,
b ] функции кусочно-гладкой функцией. Пусть функция f (x) непрерывна на сегменте [ a, b ]. Тогда для любого e > 0 существует непрерывная, кусочно-гладкая функция l (x), такая, что для любого x из сегмента [ a, b ] выполняется условие | f (x) − l (x)| < e, причём l (a) = f (a), l (b) = f (b).
Лемма 2. Если функция f (x) кусочно-непрерывна на сегменте [ a, b ], то
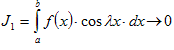 1) при l → ∞,
1) при l → ∞,
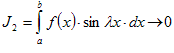 2) при l → ∞.
2) при l → ∞.
Теорема 2. О поточечной сходимости тригонометрического ряда Фурье. Пусть f (x) – кусочно-гладкая функция на сегменте [ − p; p ]. Тогда ряд
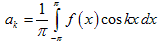
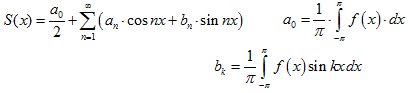 , где,,
, где,,
,
сходится в каждой точке x Î [ − p; p ], и для его суммы S (x) справедливо равенство
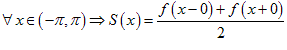 1),
1),
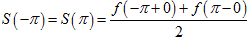 2).
2).
3. Комплексная форма ряда Фурье. Заметим, что
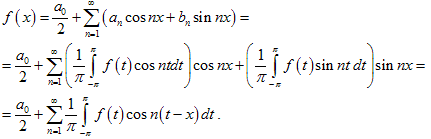 При этом
При этом
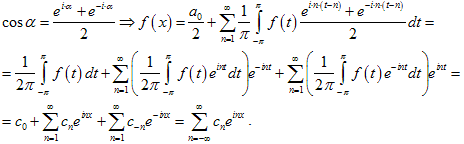 Таким образом,
Таким образом,
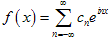
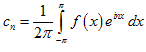 , где.
, где.
Тем самым мы получили разложение функции f (x) по системе функций { einx }. Указанная система функций является ортогональной на сегменте [ − p; p ], то есть
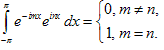 .
.
4. Понятие общего ряда Фурье по произвольной ортогональной системе функций. Тригонометрический ряд Фурье является частичным случаем общего ряда Фурье. Рассмотрим пространство кусочно-непрерывных на сегменте [ a, b ] функций Q [ a, b ]. Будем предполагать, что в точке разрыва
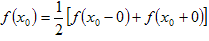 .
.
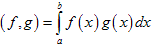 Введём в пространстве Q [ a, b ] скалярное произведение (свёртку) двух функций,
Введём в пространстве Q [ a, b ] скалярное произведение (свёртку) двух функций,
. Имеет место неравенство Коши
(f, g)2≤ (f, f) · (g, g).
Определение 4. Линейное пространство называется нормированным, если каждому элементу f поставлено в соответствие неотрицательное вещественное число − норма, || f ||, которая удовлетворяет следующим условиям:
1. || f || > 0, если f ≠ q; || f || = 0, если f = q,
2. || l · f || = | l | · || f ||, для любого числа l,
3. " f, g Þ || f + g || ≤ || f || + || g ||.
В любом нормированном пространстве можно ввести метрику, т.е. расстояние между двумя элементами, по формуле
r (f, g) = || f − g ||.
Во всяком евклидовом пространстве можно ввести норму
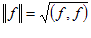 .
.
Определение 5. Последовательность элементов евклидова пространства
{ yn } называется ортонормированной, если её элементы попарно ортогональны, а норма каждого элемента равна единице.
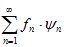 Определение 6. Рядом Фурье элемента f по ортонормированной системе
Определение 6. Рядом Фурье элемента f по ортонормированной системе
{ yn } называется ряд, где fn = (f, yn). Величины fn называются коэффициентами Фурье элемента f.
Если евклидово пространство имеет конечную размерность N, то система { yn }, состоящая из N ортогональных элементов, норма каждого из которых равна единице, образует ортонормированный базис и любой элемент f такого пространства можно разложить по этому базису
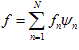 .
.
В случае бесконечной размерности евклидова пространства актуален вопрос о сходимости ряда Фурье по метрике данного пространства. Назовем величину
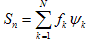 частичной суммой ряда Фурье.
частичной суммой ряда Фурье.
Наряду с Sn будем рассматривать линейные комбинации элементов ортонормированной системы
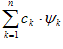 .
.
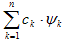 Теорема 3. При фиксированном n из всех сумм вида наименьшее
Теорема 3. При фиксированном n из всех сумм вида наименьшее
отклонение от элемента f по норме данного евклидова пространства имеет частичная сумма
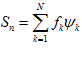 .
.
Это свойство называют экстремальным свойством ряда Фурье.
Теорема 4. Для любого элемента f, для любой ортонормированной системы { yn } и для любого n выполняется равенство (тождество Бесселя)
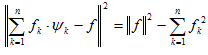 Теорема 5. Для любого элемента f, для любой ортонормированной системы { yn } справедливо неравенство (неравенство Парсеваля)
Теорема 5. Для любого элемента f, для любой ортонормированной системы { yn } справедливо неравенство (неравенство Парсеваля)
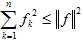 .
.
 2015-02-04
2015-02-04 3233
3233
