 1. Тригонометрический ряд Фурье
1. Тригонометрический ряд Фурье
Определение 1. Функция f (x), определённая на всей числовой прямой, называется периодической, если $ T > 0: " x Þ f (x + T) = f (x)
Если среди всех положительных периодов T имеется наименьший, то он называется наименьшим положительным периодом.
Система функций
1, cos x, sin x, cos 2 x, sin 2 x, …, cos nx, sin nx, …
называется основной тригонометрической системой функций.
В этом параграфе мы исследуем вопрос о возможности представить некоторую периодическую функцию с периодом 2 p в виде сходящегося (в некотором смысле) функционального ряда, каждый член которого является функцией основной тригонометрической системы с некоторым коэффициентом.
Будут установлены достаточные условия того, что периодическая функция f (x) может быть представлена в указанном виде,
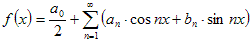 (1)
(1)
Равенство (1) называется разложением функции f (x) в тригонометрический ряд Фурье, коэффициенты an и bn называются коэффициентами Фурье функции f (x) по косинусам и по синусам. Выведем формулы для an и bn Для этого будем считать, что f (x) задана на сегменте [ − p; p ] является периодической на всей числовой оси c периодом 2 p.
Используя таблицу интегралов, установим свойство, которое называют «ортогональностью тригонометрической системы функций»,
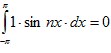 ,
,
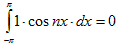 ,
,
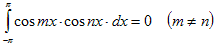 ,
,
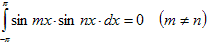 ,
,
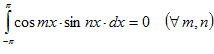 .
.
В пространстве интегрируемых функций, заданных на сегменте [ − p; p ], введем скалярное произведение функций следующим образом:
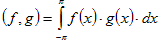 .
.
Если (f, g) = 0, то функции f и g называются ортогональными. Таким образом, основная тригонометрическая система состоит из взаимно ортогональных Функций.
Будем предполагать, что для функции f (x) справедливо равенство (1) и что этот ряд (называемый рядом Фурье) можно почленно интегрировать.
Проинтегрируем равенство (1) в пределах x Î [ − p; p ],
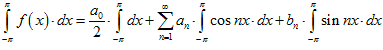 ,
,
поэтому
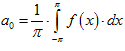 .
.
Умножим равенство (1) на cos kx и проинтегрируем в пределах x Î [ − p; p ],
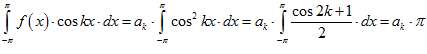 ,
,
поэтому
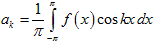 .
.
Аналогично получим
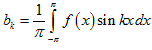 .
.
Таким образом,
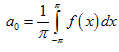
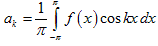
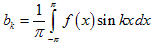 ,,.
,,.
Теорема 1. Если f (x) – периодическая функция с периодом T, то для любого числа
a имеет место равенство
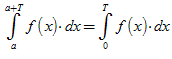 ,
,
т.е. интеграл по любому сегменту длиной в период имеет одно и тоже значение.
 2015-02-04
2015-02-04 1075
1075
