Отрезок интегрирования разбивается на четное число 2n равных частей длины h=(b-a)/2n.
a=x0 < x1 < …< x2n-1 < x2n = b
Рассматривается пара соседних участков и через три точки кривой с координатами (x0,y0), (x1,y1), (x2,y2) проводится парабола с осью, параллельной оси Oy.
Ее уравнение y=Ax2 +Bx +C. Площадь криволинейной трапеции на участке [x0,x2] заменяется площадью криволинейной трапеции, ограниченной параболой.
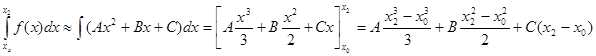
Если вынести за скобку общий множитель x2-x0 и привести к общему знаменателю, получится
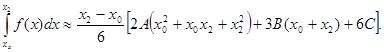 (1)
(1)
Неизвестные коэффициенты A, B, C находятся из условия, что при значениях x равных x0, x1,x2, функция f(x) принимает соответственно значения y0, y1, y2. Если взять 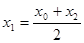 , то условия можно записать
, то условия можно записать
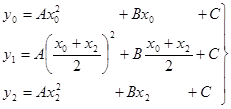 (2)
(2)
Второе равенство умножается на четыре, все три равенства складываются, получается
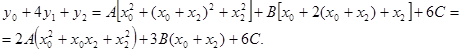 (3)
(3)
Что совпадает с квадратной скобкой в правой части равенства (1). Если подставить (3) в (1), и заметить, что x2 –x1=2h, (h=(b-a)/(2n)), то получится
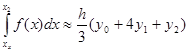 (4)
(4)
Для каждой следующей пары участков получится такая же формула
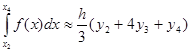 (5)
(5)
Суммируя равенства вида (4) и (5) по всем участкам можно получить
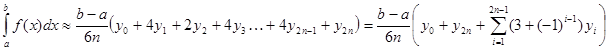
или, если обозначить N=2n
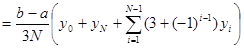 .
.
Это и есть формула Симпсона. Ее называют также формулой парабол.
 Переменная с=1 для нечетных i и –1 для четных, т.о. реализуется коэффициент (-1) i -1.
Переменная с=1 для нечетных i и –1 для четных, т.о. реализуется коэффициент (-1) i -1.
| 


|
Результаты вычисления интеграла 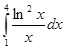 , полученные разными методами:
, полученные разными методами:
| Метод | Результат | |
| MatLab | трапеций Симпсона Лобатто | 0.88815714659999 0.88807223886900 0.88806573865982 |
| MathCad | 0.88806573863715 | |
| Трапеций | 0.88815714659998 | |
| Прямоугольников | слева справа среднее | 0.852123212814331 0.924191164970398 0.8881571888923645 |
| Симпсона | 0.888067817687988 |
 2015-02-04
2015-02-04 480
480








