Определение 4. Если всякой точке М из множества точек 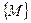 евклидового пространства
евклидового пространства 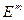 по определенному закону ставится в соответствие некоторое число u из числового множества U, то говорят, что на множестве
по определенному закону ставится в соответствие некоторое число u из числового множества U, то говорят, что на множестве 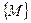 задана функция
задана функция 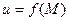 . При этом множества
. При этом множества 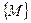 и U называют соответственно областью определения (задания) и областью изменения функции
и U называют соответственно областью определения (задания) и областью изменения функции 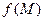 .
.
Функция одной переменной 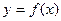 изображается на плоскости в виде линии. В случае двух переменных областью определения
изображается на плоскости в виде линии. В случае двух переменных областью определения 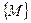 является множество точек на координатной плоскости Оху. Координата z называется аппликатой, а сама функция изображается в виде поверхности в пространстве
является множество точек на координатной плоскости Оху. Координата z называется аппликатой, а сама функция изображается в виде поверхности в пространстве 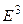 . Аналогичным образом функция m переменных, определенная на множестве
. Аналогичным образом функция m переменных, определенная на множестве 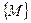 евклидового пространства
евклидового пространства 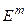 , представляет собой гиперповерхность в евклидовом пространстве
, представляет собой гиперповерхность в евклидовом пространстве 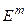 .
.
 2015-02-04
2015-02-04 192
192







