Градиент функции

Определение. Градиентом функции 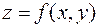называется вектор, координаты которого равны соответственно частным производным 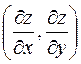. Обозначение: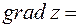 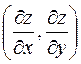. Рассмотрим скалярное произведение векторов 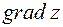и единичного вектора 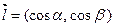. Получим 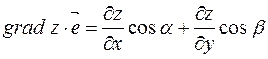. Сравнивая с формулой для производной по направлению видим, что 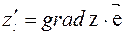, т.е. производная по направлению является скалярным произведением градиента и единичного вектора, задающего направление l. Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции 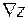в данной точке характеризует направление максимальной скорости изменения функции в этой точке.

Теорема. Пусть задана дифференцируемая функция 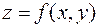и пусть в точке 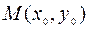величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.