Определение: Директрисами эллипса называются две прямые,
перпендикулярные к большой оси эллипса и расположенные
симметрично относительно центра на расстоянии  от него.
от него.
Если эллипс задан каноническим уравнением (8), причём a 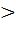 b, то в выбранной системе координат его директрисы определяются уравнениями
b, то в выбранной системе координат его директрисы определяются уравнениями 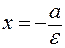 и
и 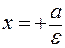 (44).
(44).
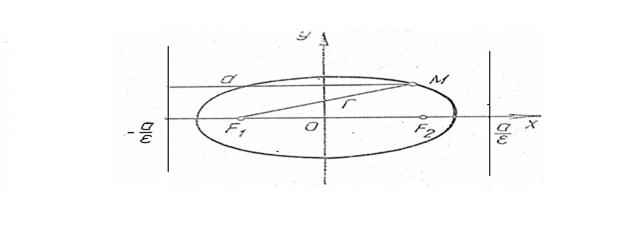
Рис. 8
Т. к. для эллипса 0 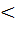 ε
ε 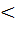 1, то
1, то 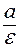
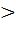 a. Это означает, что директрисы эллипса не имеют с ним общих точек.
a. Это означает, что директрисы эллипса не имеют с ним общих точек.
Определение: Директрисами гиперболы называются две прямые, перпендикулярные к большой оси гиперболы и расположенные симметрично относительно центра на расстоянии
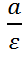 от него.
от него.
Если гипербола задана каноническим уравнением (25), то в данной системе координат её директрисы определяются уравнениями (44).
Поскольку для гиперболы ε 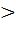 1, то
1, то 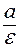
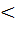 a. Это означает, что директрисы гиперболы не имеют с ней общих точек.
a. Это означает, что директрисы гиперболы не имеют с ней общих точек.
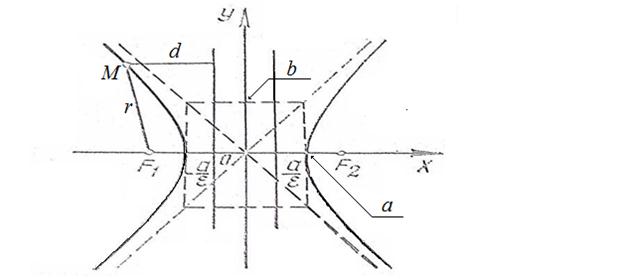
Рис. 9
Важное свойство директрис эллипса и гиперболы выражает следующая теорема.
Теорема. Отношение расстояния r произвольной точки эллипса (гиперболы) до фокуса к расстоянию d этой точки до соответствующей директрисы есть постоянная величина, равная 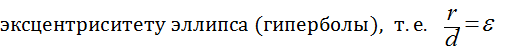
Доказательство. Рассмотрим, например, левый фокус и левую директрису эллипса. Пусть (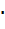 )М(х; у) – произвольная точка эллипса (рис. 8). Здесь
)М(х; у) – произвольная точка эллипса (рис. 8). Здесь
r = a + εx, d = – (–  ) = x +
) = x +  .
.
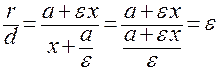
Если (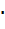 )М(х; у) – произвольная точка левой ветви гиперболы
)М(х; у) – произвольная точка левой ветви гиперболы
(Рис. 9), то
r = – εx – a, d = – x –  .
.
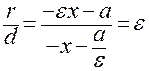 .
.
Свойство, выраженное вышеприведённой теоремой, может быть положено в основу определения эллипса и гиперболы.
Множество всех точек плоскости, для которых отношение расстояния r до фиксированной точки (фокуса) к расстоянию d до фиксированной прямой (директрисы) есть 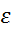 – величина постоянная. Причём фигура оказывается эллипсом при
– величина постоянная. Причём фигура оказывается эллипсом при 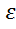
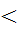 1 и – гиперболой при
1 и – гиперболой при 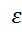
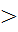 1.
1.
Вопрос о том, что представляет собой это множество точек в случае 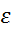
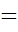 1, рассматривается в следующем параграфе.
1, рассматривается в следующем параграфе.
 2015-02-04
2015-02-04 1064
1064








