Пропорциональной зависимости

В школьной программе гипербола определяется уравнением

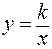(40).

Это уравнение выражает обратную пропорциональную зависи-мость переменных величин х и у. В выражении (40) нелегко распо-знать (увидеть) связь с каноническим уравнением (25) гиперболы.

При 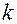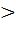0 график гиперболы имеет вид

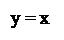
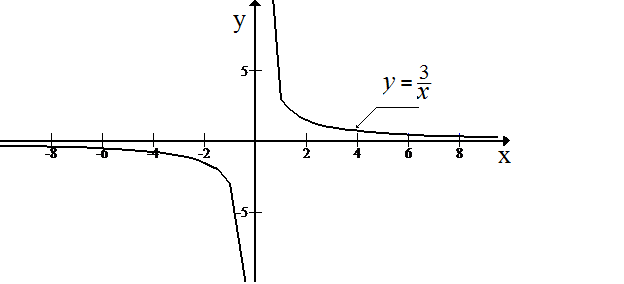
Рис. 5

Для параболы (38) центр координатной системы является центром симметрии. А прямые у = х и у = – х являются осями симметрии.

Совершим поворот осей ОХ и ОУ на 45⁰ против часовой стрелки. В матричной форме этот переход будет иметь вид

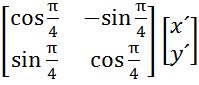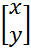= (41)

или

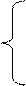
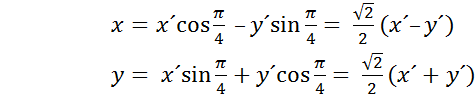(42).

Представим уравнение (38) в виде

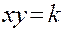(43).

Подставим в левую часть этого уравнения выражения для х и у из системы (40)

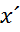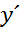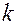[()² – ()²] = или (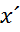)² – (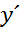)² = 2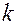

Тогда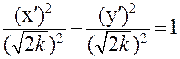

Т. е. получаем уравнение той же гиперболы (но повёрнутой на 45⁰ против часовой стрелки) в каноническом виде (Рис. 6).

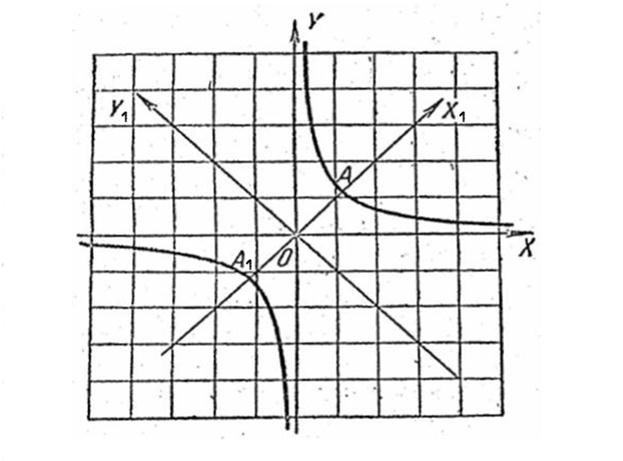
Рис. 6