Модель Кронига-Пенни

В предыдущем разделе мы рассмотрели качественную картину обобществления электронов, пользуясь моделью изолированного атома с учетом постулата Паули. Здесь воспользуемся аппаратом квантовой механики для более строгого решения этой же задачи. В общем случае задача является безнадежно сложной, и приближенное решение ее достигается путем принятия ряда упрощений.

Во-первых, будем считать, что кристалл представляет собой две подсистемы: легкие, быстрые электроны и тяжелые неподвижные ядра. Такое приближение называется адиабатическим. Оно является приемлемым, поскольку за время изменения состояния электронов состояние ядер практически не изменяется.

Однако картина остается слишком сложной. Уравнение Шредингера описывает поведение одной частицы, и вторым приближением является одноэлектронное приближение. Оно состоит в том, что электрон представляют в некоем совокупном поле, созданном другими электронами и не зависящем от мгновенного положения данного электрона.

Модель потенциального поля кристалла представляет собой линейную цепочку прямоугольных потенциальных ям глубиной U ₀, разделенных потенциальными барьерами (рис. 4.2, а). Ширина ямы b, ширина барьера d, b + d = a – период решетки.

d

в

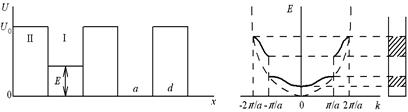
а) б)

Рис. 4.2. Электрон в кристалле: а – модель Кронига-Пенни; б – энергетический

спектр электрона

Запишем стационарное уравнение Шредингера

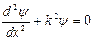. (4.1)

Решение этого уравнения имеет следующий вид:

в области ямы

ψ ₁= А ₁exp(ik ₁ x)+ B ₁exp(- ik ₁ x), (4.2)

где 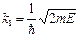, (4.3)

в области барьера

ψ ₂= А ₂exp(k ₂ x)+ B ₂exp(k ₂ x), (4.4)

где 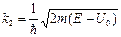. (4.5)

Очевидно, что решение уравнения (4.1) будет определяться величиной U ₀. Различают три случая, или три приближения.

Приближение свободных электронов. Потенциал решетки очень мал, U ₀à0, т.е. мы имеем электрон в нулевом потенциальном поле. Этот случай практически совпадает с уже рассмотренным в п. 2.3. Напомним, что движение электрона описывается плоской волной, а энергетический спектр является сплошным, т.е. представляет собой одну разрешенную зону. Потенциальное поле кристалла можно представить как большую яму с плоским дном.

Приближение сильносвязанных электронов. Это другой крайний случай, когда пренебрегают влиянием решетки, а U ₀= U_a – потенциал атома. Этот случай также рассмотрен в п. 2.7. Энергетический спектр электрона в этом случае линейчатый, т.е. разрешенные зоны вырождаются в энергетические уровни, а электроны локализованы в атомах.

Приближение слабосвязанных электронов. Это приближение в некотором роде описывает промежуточный случай между двумя предыдущими: приближением свободных и сильносвязанных электронов. Потенциальное поле этого приближения можно представить в виде суммы

U (x) = U ₀+ δU

где δU<< U ₀ – периодическая функция с периодом, равным периоду кристаллической решетки.

Модель потенциального поля кристалла в этом случае можно представить в виде потенциальной ямы со слабо рифленым дном. Решение уравнения Шредингера для такого поля называют функцией Блоха. Для одномерного случая она имеет вид:

ψ (x) = U (x)exp(ikx), (4.6)

где U (x) – периодическая функция, или модулирующий множитель, описывает характер дна потенциальной ямы.

Подставив (4.2) и (4.4) в выражение (4.6), можно найти конкретный вид модулирующего множителя U (x). Если учесть граничные условия для предельного случая потенциального барьера (d "0, U ₀"∞), можно получить выражение

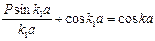, (4.7)

где 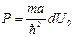– характеристика прозрачности барьера.

Уравнение (4.7) выражает зависимость энергии электрона Е, входящей в соотношение (4.3), от волнового вектора k для барьеров различной прозрачности Р. Графическое решение уравнения (4.7) позволяет сделать следующие выводы.

Функция Е (k) в точках πn / a имеет разрывы, соответствующие запрещенным зонам. Области, где Е (k) непрерывна, соответствуют разрешенным зонам. Особенно наглядно это можно представить, если спроектировать функцию Е (k) на вертикаль. На рис. 4.2, б показан график функции Е (k). Штрих-пунктиром показана функция для свободного электрона. На рисунке видно, что с увеличением энергии электрона ширина запрещенных зон уменьшается, а ширина разрешенных зон увеличивается. Ширина зон зависит также от параметра P в (4.7). В случае P "∞ разрешенные зоны сужаются, превращаясь в дискретные уровни, соответствующие k ₁ a = πn, т.е. в уровни потенциальной ямы. При P "0 потенциальные барьеры исчезают, электрон становится свободным.