Задача 1. На наклонной плоскости, составляющей с горизонтом угол a=300, находится груз массой m2=2кг. К грузу привязан легкий шнур, перекинутый через блок, укрепленный на вершине наклонной плоскости. К другому концу шнура подвешена гиря массой m1=20кг. Предоставленная самой себе, система приходит в равноускоренное движение. Определите ускорение грузов и силу давления на ось блока при условии, что коэффициент трения между грузом и плоскостью равен m=0,1. массу блока не учитывать.
Дано: a=300; m1=20кг; m2=2кг; m=0,1; 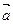 =const
=const
Найти: F д –?
 Решение:
Решение:
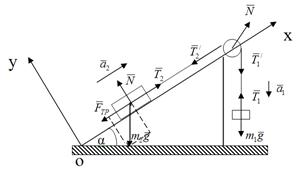
Укажем внешние силы, действующие на каждое из тел системы. Очевидно, гиря будет опускаться, а груз будет подниматься по наклонной плоскости. Рассмотрим движение гири. На гирю действует сила тяжести 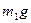 и сила натяжения шнура
и сила натяжения шнура 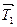 . Поскольку гиря опускается ускоренно, то
. Поскольку гиря опускается ускоренно, то
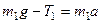
На груз действует сила тяжести 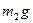 , сила натяжения шнура
, сила натяжения шнура 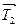 , сила трения
, сила трения 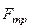 и нормальная реакция опоры
и нормальная реакция опоры 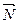 . Выберем систему отсчета – наклонную плоскость и связанную с ней систему координат. Ось Ох направим вдоль наклонной плоскости в сторону движения груза, ось Оу – перпендикулярно наклонной плоскости. Под действием приложенных сил груз массой m2 ускоренно поднимается по наклонной плоскости, поэтому основное уравнение динамики в проекциях на ось Ох имеет вид:
. Выберем систему отсчета – наклонную плоскость и связанную с ней систему координат. Ось Ох направим вдоль наклонной плоскости в сторону движения груза, ось Оу – перпендикулярно наклонной плоскости. Под действием приложенных сил груз массой m2 ускоренно поднимается по наклонной плоскости, поэтому основное уравнение динамики в проекциях на ось Ох имеет вид:
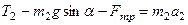
Так как груз и гиря связаны между собой, то а1=а2=а и Т1=Т2=Т
Сила трения, равная 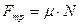 , отсутствует в направлении, перпендикулярном наклонной плоскости (Оу), поэтому
, отсутствует в направлении, перпендикулярном наклонной плоскости (Оу), поэтому
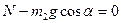
По условию задачи масса блока не учитывается, поэтому на него действует только две силы натяжения со стороны шнура (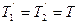 ) и нормальная реакция опоры N1 со стороны оси. Согласно третьему закону Ньютона блок действует на ось с такой же по модулю силой, но направленной в противоположную сторону. Эту силу нам надо определить.
) и нормальная реакция опоры N1 со стороны оси. Согласно третьему закону Ньютона блок действует на ось с такой же по модулю силой, но направленной в противоположную сторону. Эту силу нам надо определить.
Под действием приложенных сил блок находится в равновесии: его ускорение равно нулю 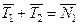 . Как видно из рис., диагональ параллелограмма равна, построенного на
. Как видно из рис., диагональ параллелограмма равна, построенного на 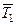 и
и 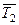 , равна по модулю
, равна по модулю 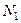
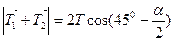 ,
,
Следовательно 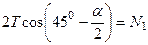
Составим систему уравнений для неизвестных величин: Т, а, N, N1
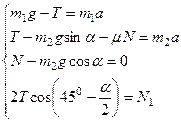
Решая эту систему относительно а, N1 получим
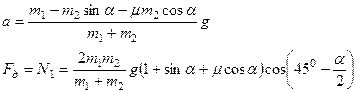
Проверим размерность: 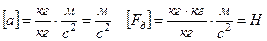
Вычисляем: а=4 м/с2; F д =202Н
Задача 2. Материальная точка колеблется согласно уравнению 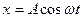 , где А =5см, w=p/12 с-1. Когда возвращающая сила F в первый раз достигает значение -12мН, потенциальная энергия Ер точки оказывается равной 0,15мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу wt.
, где А =5см, w=p/12 с-1. Когда возвращающая сила F в первый раз достигает значение -12мН, потенциальная энергия Ер точки оказывается равной 0,15мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу wt.
Дано: 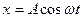 ; А =5см=5.10-2м; w=p/12с-1; F=-12мН=-1,2.10-2Н; Ер=0,15мДж=1,5.10-3Дж
; А =5см=5.10-2м; w=p/12с-1; F=-12мН=-1,2.10-2Н; Ер=0,15мДж=1,5.10-3Дж
Найти: t, wt –?
Решение: Материальная точка совершает гармонические колебания под действием силы упругости равной
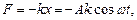
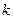 – коэффициент жесткости.
– коэффициент жесткости.
Потенциальная энергия точки 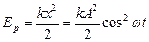
Составим отношение 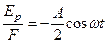 отсюда время
отсюда время 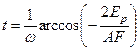
Фаза к моменту времени 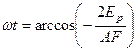
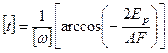
Проверка размерности: 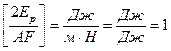
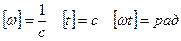
Вычисляем: 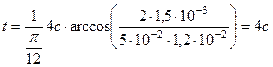
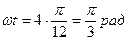
Задача 3. Определите, какую ускоряющую разность потенциалов должен пройти электрон, чтобы его продольные размеры уменьшились в два раза.
Дано: 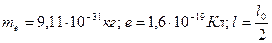
Найти: U –?
Решение: Согласно специальной теории Эйнштейна,
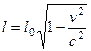 ;
; 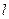 – продольный размер в системе отсчета, относительно которой электрон движется со скоростью
– продольный размер в системе отсчета, относительно которой электрон движется со скоростью 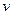 ;
; 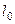 – продольный размер электрона в системе отсчета, связанной с ним. Подставляем значение l
– продольный размер электрона в системе отсчета, связанной с ним. Подставляем значение l 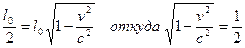
В ускоряющем электрическом поле электрон получает кинетическую энергию, равную 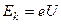
С другой стороны, согласно СТО 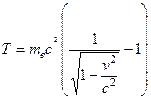
Следовательно 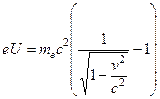
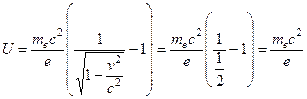
Проверяем размерность 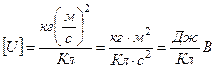
Вычисляем: 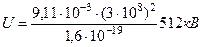
Задача 4. Поперечная волна распространяется вдоль упругого шнура со скоростью n=10м/с. Амплитуда колебаний точек шнура А=5см., период колебаний Т=1с. Запишите уравнение волны и определите: 1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии х1=9м от источника колебаний в момент времени t1=2,5с.
Дано: n=10м/с; А=5см=0,05м; Т=1с; х1=9м; t1=2,5с.
Найти: 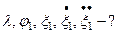
Решение: Запишем уравнение волны 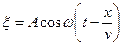
Круговая частота и длина волны связаны с периодом 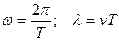 , их выражение для w подставляем в уравнение волны
, их выражение для w подставляем в уравнение волны 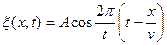
Аргумент косинуса в момент времени 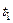 есть фаза колебаний в этот момент:
есть фаза колебаний в этот момент: 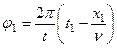 .
.
Смещение в момент 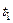
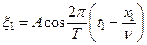
Производная от 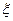 по времени есть скорость точки
по времени есть скорость точки
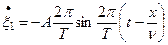 и в момент
и в момент 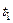 на расстоянии
на расстоянии 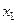 –
–
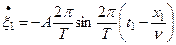
Берем еще раз производную от скорости 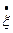 и находим ускорение этой точки
и находим ускорение этой точки
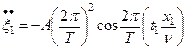
Проверка размерности: 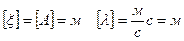
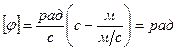
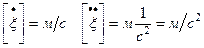
Вычисляем: 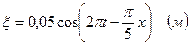
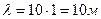
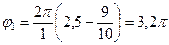
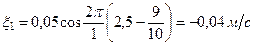
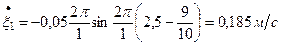
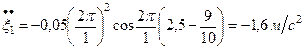
Задача 5. После упругого столкновения частицы 1 с покоившейся частицей 2 обе частицы разлетелись симметрично относительно первоначального направления движения частицы 1, и угол между их направлениями разлета 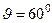 . Найти отношение масс этих частиц.
. Найти отношение масс этих частиц.
Дано: 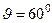 ,
, 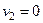
Найти: 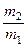 –?
–?
Решение:
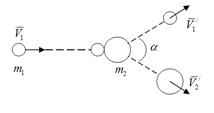
Обозначим скорости после столкновения через 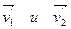
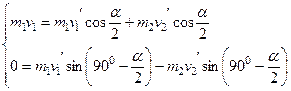
Из уравнения следует, что скорость второго тела 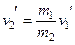
Возведем в квадрат первое уравнение системы, предварительно разделив его на массу 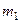 , а второе разделим на
, а второе разделим на 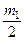 .
.
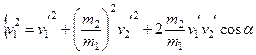
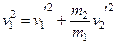
Решаем систему и получаем следующее уравнение:
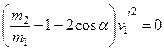 так как
так как 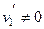 , то
, то 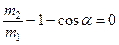 ,
,
откуда 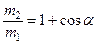 .
.
Вычисляем: 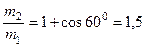
Ответ: 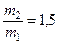 .
.
Задача 6. Маховик в виде сплошного диска, момент инерции которого J =1,5кг.м2, вращаясь при торможении равнозамедленно, за время t=1мин уменьшил частоту своего вращения с n0=240об/мин до n1=120об/мин. Определите:
1) угловое ускорение маховика ε; 2) момент силы торможения; 3) работу торможения
Дано: J =1,5кг.м2; t=1мин=60с; n0=240об/мин=4об/с; n1=120об/мин=2об/с
Найти: ε; М; А –?
Решение: Угловая скорость при равнозамедленном движении 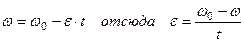 (1)
(1)
Угловая скорость выражается через частоту оборотов
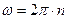 ,
, 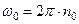 (2)
(2)
Подставляем выражения (2) в формулу (1) 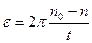
На основе уравнения динамики вращательного движения определяем момент силы 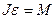
Работа равна изменению кинетической энергии маховика
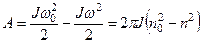
Проверяем размерность: 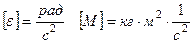

Ответ: 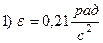
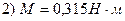
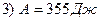
 2015-02-04
2015-02-04 7618
7618
