Задача 1. Вычислить предел последовательности с общим членом

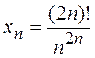 ,
,
используя теорему о пределе монотонной последовательности.
Решение. Сначала исследуем последовательность на монотонность. Для этого преобразуем выражение для 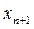 :
:
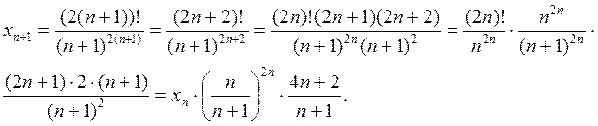
Вычислим пределы второго и третьего множителя полученного произведения:
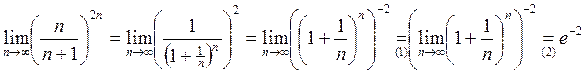
{ (1) – знак предела можно вносить под знак элементарной функции 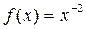 ;
;
(2) – второй замечательный предел };
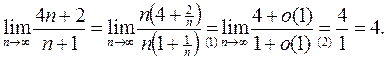
{ (1) – последовательность 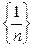 – бесконечно малая, как эталонная, последовательность
– бесконечно малая, как эталонная, последовательность 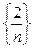 – бесконечно малая, как произведение постоянной и бесконечно малой;
– бесконечно малая, как произведение постоянной и бесконечно малой;
(2) – 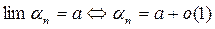 и теорема о пределе частного }
и теорема о пределе частного }
Итак, для данной последовательности имеем рекуррентное соотношение
|
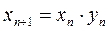 ,
, где 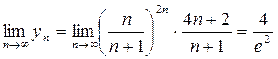 { теорема о пределе произведения }.
{ теорема о пределе произведения }.
Так как предел последовательности 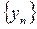 меньше 1, то и члены последовательности, начиная с некоторого номера
меньше 1, то и члены последовательности, начиная с некоторого номера 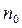 , удовлетворяют тому же неравенству:
, удовлетворяют тому же неравенству: 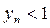 . Очевидно, что члены данной последовательности положительны, поэтому из (1) получаем:
. Очевидно, что члены данной последовательности положительны, поэтому из (1) получаем:
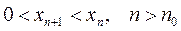 .
.
Таким образом, последовательность 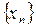 ограничена снизу и убывает, начиная с некоторого номера. Следовательно, по теореме о пределе монотонной последовательности { всякая ограниченная монотонная последовательность имеет конечный предел } существует
ограничена снизу и убывает, начиная с некоторого номера. Следовательно, по теореме о пределе монотонной последовательности { всякая ограниченная монотонная последовательность имеет конечный предел } существует
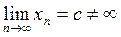 .
.
Перейдем к пределу в рекуррентном соотношении (1): 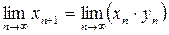
Предел, стоящий в левой части этого равенства также равен 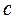 , т.к.
, т.к. 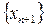 пробегает те же значения, что и
пробегает те же значения, что и 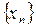 (с точностью до 1го члена). Для вычисления предела, стоящего в правой части, имеем право воспользоваться теоремой о пределе произведения { предел произведения сходящихся последовательностей равен произведению их пределов }
(с точностью до 1го члена). Для вычисления предела, стоящего в правой части, имеем право воспользоваться теоремой о пределе произведения { предел произведения сходящихся последовательностей равен произведению их пределов }
Итак, имеем
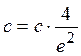 .
.
Отсюда получаем 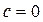 .
.
Ответ: 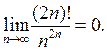
Задача 2. Вычислить предел последовательности с общим членом
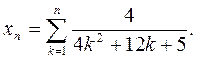
Решение. Каждую дробь-слагаемое в выражении для 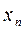 можно представить в виде суммы (или разности) дробей. Для этого знаменатель дроби разложим на множители (предварительно найдя корни соответствующего квадратного уравнения):
можно представить в виде суммы (или разности) дробей. Для этого знаменатель дроби разложим на множители (предварительно найдя корни соответствующего квадратного уравнения):
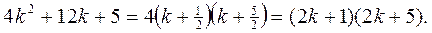
После этого можем записать 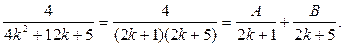 Чтобы найти коэффициенты
Чтобы найти коэффициенты 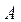 и
и 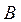 , приведем сумму дробей к общему знаменателю и приравняем числители полученной дроби и исходной:
, приведем сумму дробей к общему знаменателю и приравняем числители полученной дроби и исходной:
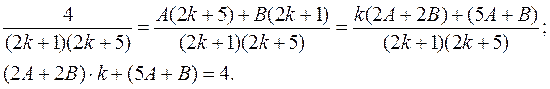
Равенство числителей есть не что иное, как тождественное равенство двух многочленов (от переменной 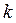 ). Отсюда следует, что соответствующие коэффициенты этих многочленов равны. Получаем систему:
). Отсюда следует, что соответствующие коэффициенты этих многочленов равны. Получаем систему:
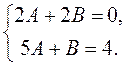
Решив ее, получаем: 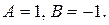
Итак, каждое слагаемое в выражении для  можно записать в виде разности 2х дробей
можно записать в виде разности 2х дробей
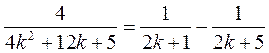 .
.
Тогда для общего члена данной последовательности имеем:
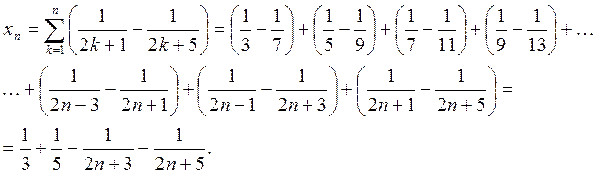
Теперь легко найти искомый предел
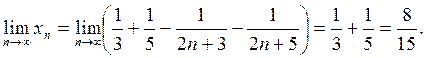
{последовательность с общим членом 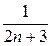 является бесконечно малой, ибо
является бесконечно малой, ибо
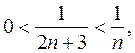
а 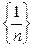 – эталонная бесконечно малая;
– эталонная бесконечно малая;
аналогично и  также бесконечно малая}.
также бесконечно малая}.
Ответ: 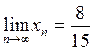 .
.
Задача 3. Найти предел последовательности с общим членом
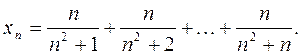
Решение. В записи для 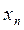 каждое из слагаемых не меньше последнего слагаемого и не больше первого. Поэтому, заменяя каждое из
каждое из слагаемых не меньше последнего слагаемого и не больше первого. Поэтому, заменяя каждое из 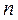 слагаемых первым или последним, получим для общего члена данной последовательности двойную оценку
слагаемых первым или последним, получим для общего члена данной последовательности двойную оценку
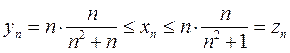 .
.
Вычислим пределы крайних членов этого двойного неравенства:
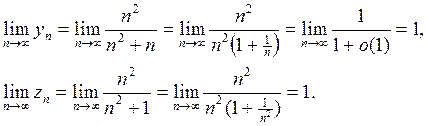
Используя достаточное условие сходимости делаем вывод: 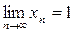 .
.
{Достаточное условие сходимости: если члены трех последовательностей удовлетворяют неравенству 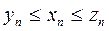 и последовательности
и последовательности 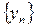 и
и 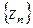 имеют один и тот же предел
имеют один и тот же предел 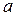 , то и последовательность
, то и последовательность 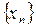 имеет “число”
имеет “число” 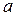 своим пределом }.
своим пределом }.
Ответ: 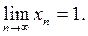
Задача 4. Доказать сходимость последовательности с общим членом
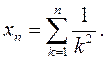
Решение. Учитывая запись для общего члена
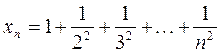 ,
,
получим рекуррентное соотношение 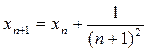 , из которого следует неравенство
, из которого следует неравенство 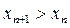 . Итак, данная последовательность монотонно возрастает. Далее, учитывая, что
. Итак, данная последовательность монотонно возрастает. Далее, учитывая, что 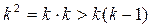 , получим для каждого слагаемого в выражении для
, получим для каждого слагаемого в выражении для 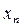 оценку
оценку
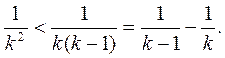
Отсюда нетрудно получить оценку и для 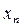
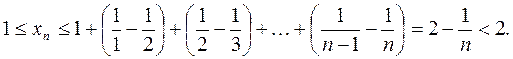
Итак, данная последовательность ограниченная. Учитывая доказанную выше монотонность, можно сказать: на основании теоремы о пределе монотонной последовательности данная последовательность имеет конечный предел, т.е. сходится, что и требовалось доказать.
Задача 5. Вычислить предел последовательности с общим членом
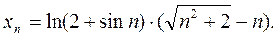
Решение. Данная последовательность есть произведение двух последовательностей с общими членами
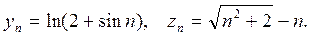
Известно, что 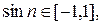 значит
значит 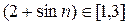 . Следовательно,
. Следовательно, 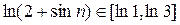 (в силу монотонности логарифмической функции). Другими словами, последовательность
(в силу монотонности логарифмической функции). Другими словами, последовательность 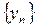 – ограничена. Последовательности
– ограничена. Последовательности 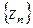 преобразуем таким образом:
преобразуем таким образом:
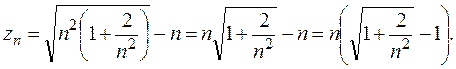
К выражению, стоящему в скобках, можно применить эквивалентность для степенной функции, а именно:
 при
при 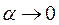 .
.
В нашем случае 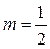 , а
, а 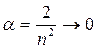 при
при 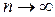 . Итак,
. Итак, 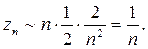 Отсюда следует, что
Отсюда следует, что 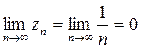 { При вычислении пределов произведений и частных каждый член произведения или частного можно заменять эквивалентным ему выражением }.
{ При вычислении пределов произведений и частных каждый член произведения или частного можно заменять эквивалентным ему выражением }.
Таким образом, 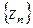 – бесконечно малая и данная последовательность
– бесконечно малая и данная последовательность 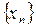 есть произведение ограниченной последовательности
есть произведение ограниченной последовательности 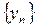 и бесконечно малой
и бесконечно малой 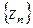 . Следовательно,
. Следовательно, 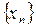 – бесконечно малая { Произведение бесконечно малой на ограниченную есть бесконечно малая }.
– бесконечно малая { Произведение бесконечно малой на ограниченную есть бесконечно малая }.
Замечание. Тот факт, что 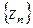 есть бесконечно малая, можно доказать и другим способом: путем умножения и деления
есть бесконечно малая, можно доказать и другим способом: путем умножения и деления 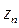 на выражение сопряженное
на выражение сопряженное 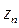 , т.е. на
, т.е. на 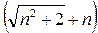 . Однако, прием, использованный при решении задачи, применим к корням любой степени.
. Однако, прием, использованный при решении задачи, применим к корням любой степени.
Ответ: 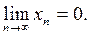
Задача 6. Вычислить пределы
a) 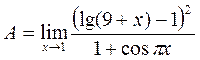 ; b)
; b) 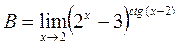 .
.
Решение. a) В данном пределе переменная не стремится к нулю и использование эквивалентностей затруднительно. Поэтому вводим новую переменную 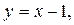 которая стремится к 0 при
которая стремится к 0 при 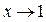 . Тогда
. Тогда 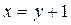 и предел принимает вид:
и предел принимает вид:
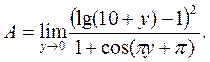
Числитель преобразуем используя свойства логарифмов, а в знаменателе применим формулу приведения:
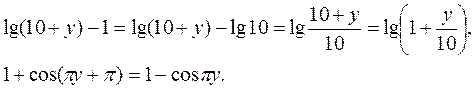
Предел принимает вид
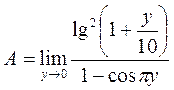 .
.
Теперь можно использовать эквивалентности для логарифма и косинуса, а именно: при 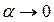
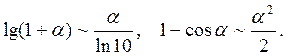
Окончательно имеем
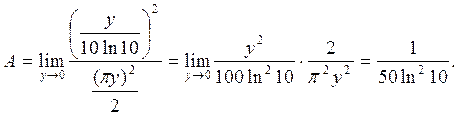
Замечание. Вообще говоря, из эквивалентности 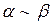 не следует эквивалентность
не следует эквивалентность 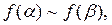 т.е. использование эквивалентностей под знаком функций недопустимо. Однако, если
т.е. использование эквивалентностей под знаком функций недопустимо. Однако, если 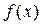 – степенная функция, этот запрет недействителен в силу непрерывности степенной функции и одного из свойств степени:
– степенная функция, этот запрет недействителен в силу непрерывности степенной функции и одного из свойств степени:
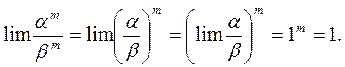
b) Функция, стоящая под знаком предела – сложная степенно-показательная функция. Для работы с такой функцией используют основное логарифмическое тождество
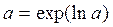
и непрерывность показательной функции
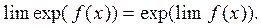
Имеем в нашем случае:
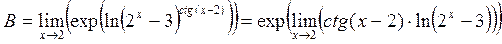 .
.
Чтобы воспользоваться эквивалентностью для логарифма (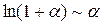 при
при 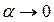 ), запишем выражение, стоящее под знаком
), запишем выражение, стоящее под знаком 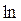 в требуемой форме
в требуемой форме
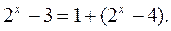
Теперь 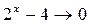 при
при 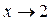 и поэтому
и поэтому
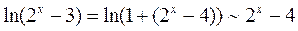 .
.
Эквивалентность для показательной функции имеет вид
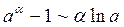 при
при 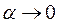 .
.
Тогда 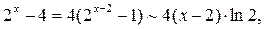 т.к.
т.к. 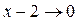 при
при 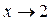 . Итак, имеем для логарифма
. Итак, имеем для логарифма 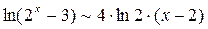 при
при 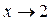 . Кроме того,
. Кроме того,
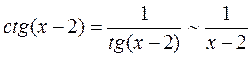 при
при 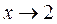
(в силу эквивалентности для тангенса 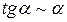 при
при 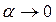 ). Окончательно имеем
). Окончательно имеем
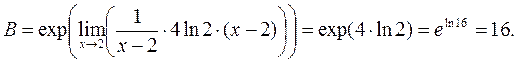
Ответ: a) 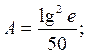
b) 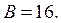
Задача 7. Исследовать на непрерывность функцию
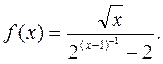
Показать графически поведение функции в окрестностях точек разрыва.
Решение. Данная функция – элементарная, поэтому непрерывна в любой точке, входящей в область определения с некоторой окрестностью. Точками же разрыва являются точки, не входящие в область определения, но такие, в окрестности которых функция определена. Область определения этой функции
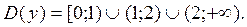
Итак, точки разрыва – это 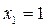 и
и 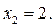
Выясним характер точек разрыва, для чего вычислим односторонние пределы данной функции в каждой из этих точек.
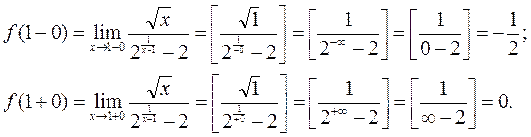
Т.к. в точке 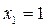 существуют конечные, но не равные односторонние пределы, то эта точка является точкой разрыва 1го рода.
существуют конечные, но не равные односторонние пределы, то эта точка является точкой разрыва 1го рода.
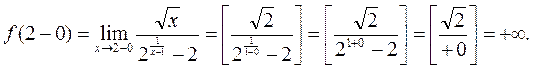
Т.к. найденный левый предел функции равен бесконечности, то и без вычисления правого предела можно сказать, что точка 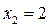 – это точка разрыва 2го рода { точка
– это точка разрыва 2го рода { точка 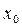 называется точкой разрыва 2го рода, если хотя бы один из пределов
называется точкой разрыва 2го рода, если хотя бы один из пределов 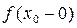 и
и 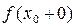 равен бесконечности или не существует }. Однако, для выяснения поведения функции в окрестности точки разрыва необходимо найти и правый предел. Нетрудно видеть, что
равен бесконечности или не существует }. Однако, для выяснения поведения функции в окрестности точки разрыва необходимо найти и правый предел. Нетрудно видеть, что 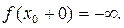
Графическое изображение поведения функции в окрестностях точек разрыва:
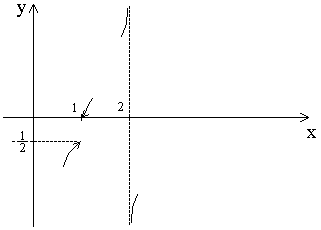
Ответ: Данная функция непрерывна на 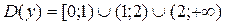 (как элементарная); в точке
(как элементарная); в точке 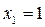 она имеет разрыв 1го рода (скачок), в точке
она имеет разрыв 1го рода (скачок), в точке 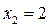 – разрыв 2го рода (бесконечный разрыв).
– разрыв 2го рода (бесконечный разрыв).
Задача 8. Исследовать на непрерывность функцию
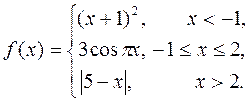
Решение. Данная функция, вообще говоря, не является элементарной, ибо задана несколькими аналитическими выражениями, а не одним. Поэтому она может иметь разрывы и в точках, принадлежащих ее области определения. Однако, каждое из 3х выражений, которыми задана функция, является элементарным, а следовательно и непрерывным на своей области задания. Поэтому точками разрыва могут быть лишь точки, в которых функция меняет одно выражение на другое. Итак, возможные точки разрыва данной функции – это точки 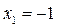 и
и 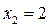 . Исследуем эти точки.
. Исследуем эти точки.
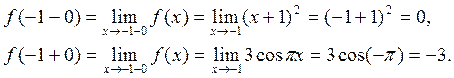
Односторонние пределы существуют, конечны, но различны по величине, следовательно 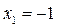 – точка разрыва 1го рода. Говорят, что функция имеет в точке
– точка разрыва 1го рода. Говорят, что функция имеет в точке 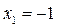 скачок равный
скачок равный 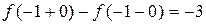 .
.
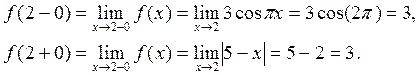
Совпадение односторонних пределов означает, что предел функции в т. 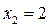 существует, причем
существует, причем 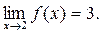 Вычислим еще и значение функции в точке
Вычислим еще и значение функции в точке 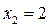 :
:
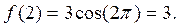
Т.к. 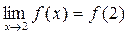 , то делаем вывод: данная функция непрерывна в т.
, то делаем вывод: данная функция непрерывна в т. 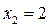 (по определению).
(по определению).
Ответ: Данная функция непрерывна всюду за исключением точки 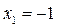 , в которой она имеет разрыв 1го рода.
, в которой она имеет разрыв 1го рода.
Задача 9. Построить график функции
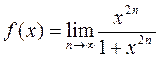
и указать ее точки разрыва.
Решение. При каждом фиксированном 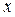 последовательность
последовательность 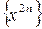 есть эталонная типа
есть эталонная типа 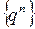 . Её поведение зависит от величины
. Её поведение зависит от величины 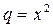 , а именно: при
, а именно: при 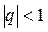 – это бесконечно малая последовательность, а при
– это бесконечно малая последовательность, а при 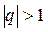 – бесконечно большая. Таким образом, для
– бесконечно большая. Таким образом, для 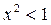 , т.е. для
, т.е. для 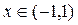 , имеем:
, имеем:
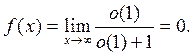
Далее, пусть 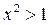 , т.е.
, т.е. 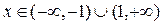 . Тогда
. Тогда
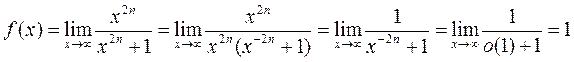
(очевидно, что, если 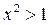 , то
, то 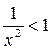 и
и 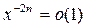 ). Остается рассмотреть случай
). Остается рассмотреть случай 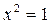 , т.е.
, т.е. 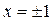 . В этом случае
. В этом случае
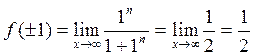
{предел постоянной равен ей самой}. Итак, окончательно имеем:
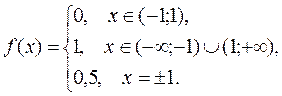
График имеет вид
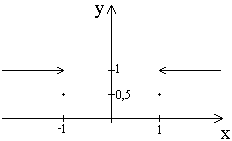
Ответ: Функция непрерывна всюду, за исключением точек 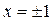 , в которых она имеет разрыв 1го рода.
, в которых она имеет разрыв 1го рода.
Задача 10. Функцию
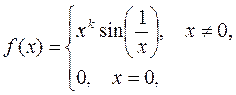
исследовать на: 1) непрерывность; 2) дифференцируемость; 3) непрерывную-дифференцируемость.
Решение. 1) Данная функция может иметь разрыв лишь в точке 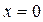 (см. задачу 8). Для
(см. задачу 8). Для 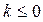 функция имеет в этой точке разрыв 2го рода, ибо представляет собой произведение множителя
функция имеет в этой точке разрыв 2го рода, ибо представляет собой произведение множителя 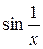 , который не имеет предела при
, который не имеет предела при 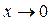 , и постоянной (
, и постоянной (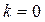 ) или бесконечно большой (
) или бесконечно большой (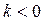 ).
).
Для 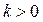 функция является бесконечно малой при
функция является бесконечно малой при 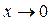 , как произведение эталонной бесконечно малой
, как произведение эталонной бесконечно малой 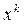 и ограниченной
и ограниченной 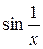 . Значит, для
. Значит, для 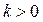
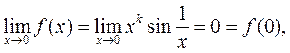
что означает непрерывность 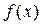 в т.
в т. 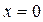 .
.
2) Исследуем функцию на дифференцируемость, то есть на существование конечной производной.
Для значений 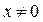 производную вычисляем используя правила дифференцирования и таблицу производных:
производную вычисляем используя правила дифференцирования и таблицу производных:
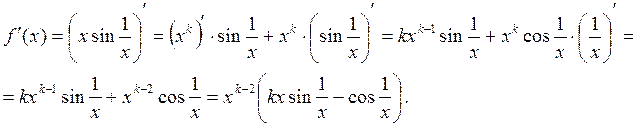
Это выражение для 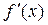 справедливо для любых значений параметра.
справедливо для любых значений параметра.
Производную в нуле вычисляем по определению (нельзя писать 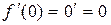 , ибо значение 0 функция принимает в одной точке
, ибо значение 0 функция принимает в одной точке 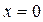 , а не в некоторой ее окрестности):
, а не в некоторой ее окрестности):
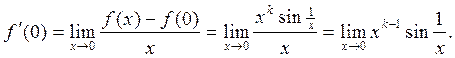
Ситуация с этим пределом аналогична рассмотренной в предыдущем пункте: при 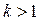 искомая производная равна 0, а при
искомая производная равна 0, а при 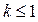 – не существует.
– не существует.
Итак, для 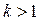
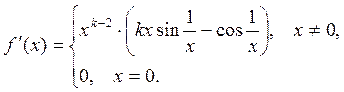
3) Исследуем производную 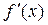 на непрерывность. Возможная точка разрыва –
на непрерывность. Возможная точка разрыва – 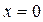 .
.
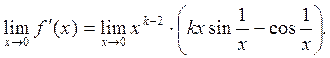
Если 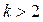 , то этот предел равен 0, т.е. равен
, то этот предел равен 0, т.е. равен 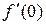 , что означает непрерывность производной в нуле. Если же
, что означает непрерывность производной в нуле. Если же 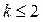 , данный предел не существует (выражение в скобках не имеет предела из-за
, данный предел не существует (выражение в скобках не имеет предела из-за 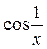 ).
).
Замечание. Производную 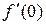 можно вычислить не по определению, а применив теорему о пределе производной: если
можно вычислить не по определению, а применив теорему о пределе производной: если 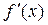 существует для
существует для 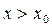 и если существует
и если существует 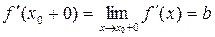 , то существует и правая производная в т.
, то существует и правая производная в т. 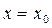 , причем
, причем 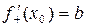 (аналогичное утверждение справедливо и для левой производной). Для данной функции эта теорема срабатывает при
(аналогичное утверждение справедливо и для левой производной). Для данной функции эта теорема срабатывает при 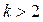 . Для
. Для 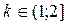 приходится пользоваться определением при вычислении
приходится пользоваться определением при вычислении 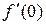 .
.
Ответ: 1) Функция непрерывна всюду при 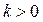 . При
. При 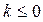 имеем разрыв 2го рода в точке
имеем разрыв 2го рода в точке 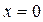 .
.
2) Функция дифференцируема всюду при 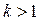 , при этом
, при этом
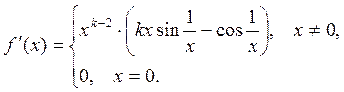
3) Функция непрерывно-дифференцируема при 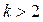 .
.
Задача 11. Найти 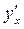 для функций, заданной параметрически и неявно:
для функций, заданной параметрически и неявно:
а) 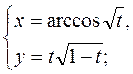 b)
b) 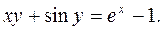
Решение. a) Если функция задана параметрически уравнениями
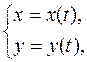
то её производная 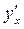 задается следующей системой параметрических уравнений
задается следующей системой параметрических уравнений
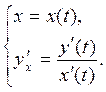
В нашем случае:
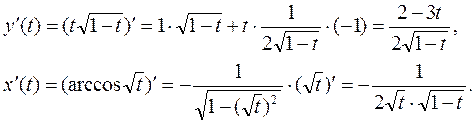
Поэтому искомая производная имеет вид:
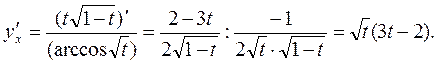
b) При вычислении производной функции, заданной неявно, используют следующие соображения.
При некоторых условиях на выражения с двумя переменными 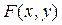 (эти условия рассматриваются в теме “Функции нескольких переменных”) уравнение вида
(эти условия рассматриваются в теме “Функции нескольких переменных”) уравнение вида
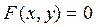
разрешимо относительно переменной 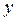 . Это означает следующее: существует дифференцируемая функция
. Это означает следующее: существует дифференцируемая функция 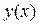 такая, что имеет место тождество
такая, что имеет место тождество
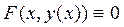
в некотором интервале изменения переменной 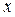 . Дифференцируя это тождество по переменной
. Дифференцируя это тождество по переменной 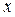 , получим соотношение, из которого легко находится искомая производная
, получим соотношение, из которого легко находится искомая производная 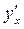 . Ясно, что подобные рассуждения применимы и для уравнений вида
. Ясно, что подобные рассуждения применимы и для уравнений вида 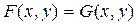 .
.
Итак, считая, что в данном уравнении 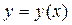 и рассматривая его как тождество, получим:
и рассматривая его как тождество, получим:
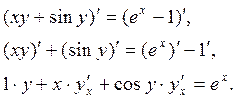
Отсюда и получаем
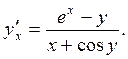
Ответ: a) 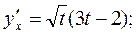 b)
b) 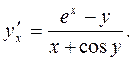
Задача 12. Найти производную 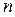 -го порядка функции
-го порядка функции
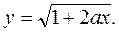
Решение. По определению производная 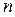 -го порядка – это производная от производной
-го порядка – это производная от производной 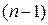 -го порядка:
-го порядка:
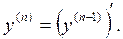
Вычислим производные 1го, 2го, 3го порядка и попытаемся уловить закономерность:
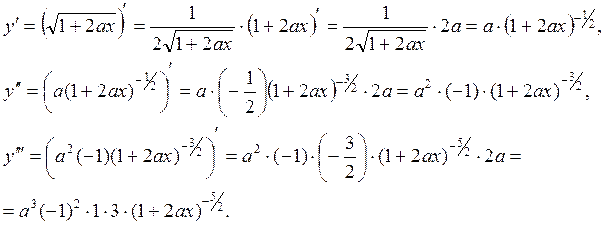
Можно предположить, что
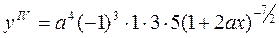
и, вообще,
|
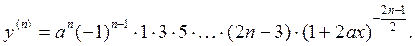
Чтобы доказать истинность нашего предположения, найдем производную 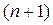 -го порядка, считая, что формула (*) верна.
-го порядка, считая, что формула (*) верна.
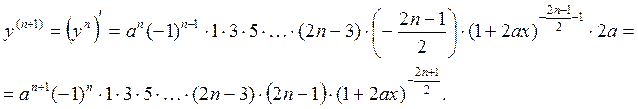
Нетрудно заметить, что это выражение для 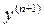 можно получить из (*) заменив
можно получить из (*) заменив 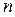 на
на 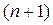 . Это и доказывает верность формулы (*).
. Это и доказывает верность формулы (*).
Замечание 1. Формула (*) верна для 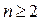 .
.
Замечание 2. Для произведения всех нечетных чисел от 1 до 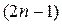 принято обозначение
принято обозначение 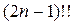 . Таким образом,
. Таким образом, 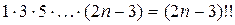 .
.
Ответ: 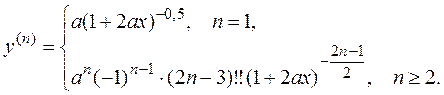
Задача 13. Раскрыть неопределенности:
a) 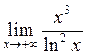 ; b)
; b) 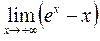 c)
c) 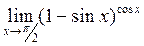 .
.
Решение. Сделаем несколько общих замечаний о применении правила Бернулли-Лопиталя.
1. Правило Бернулли-Лопиталя вычисления предела отношения двух бесконечно больших или бесконечно малых функций состоит в замене отношения функций отношением их производных.
2. Это правило применимо лишь к неопределенностям вида 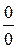 или
или 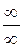 , а неопределенности других типов (
, а неопределенности других типов (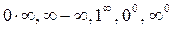 ) необходимо сводить к этим двум.
) необходимо сводить к этим двум.
3. Иногда для раскрытия неопределенности приходится применять это правило последовательно несколько раз.
4. На каждом этапе применения правила Бернулли-Лопиталя следует пользоваться тождественными преобразованиями, а также комбинировать это правило с другими приёмами вычисления пределов (замена переменной, эквивалентности и т.п.).
Перейдем к вычислению пределов:
a) 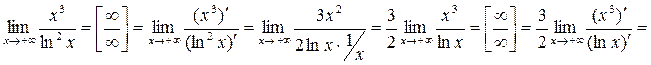
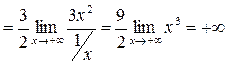 .
.
b) 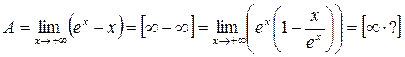
Вычислим отдельно:
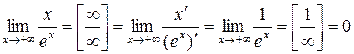 .
.
Значит, 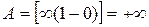 .
.
c) 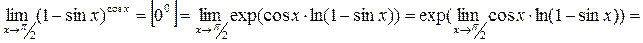
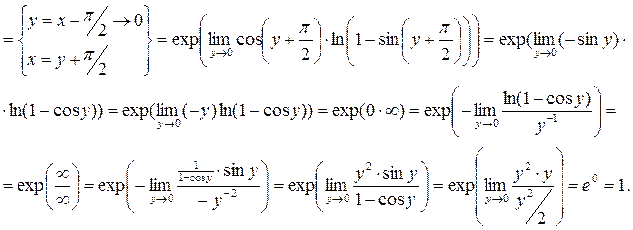
При вычислении этого предела последовательно использованы: основное логарифмическое тождество; непрерывность функции 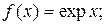 замена переменной; формулы приведения; эквивалентность
замена переменной; формулы приведения; эквивалентность 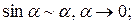 преобразование неопределенности
преобразование неопределенности 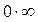 в неопределенность
в неопределенность 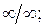 правило Бернулли-Лопиталя; тождественные преобразования; эквивалентность
правило Бернулли-Лопиталя; тождественные преобразования; эквивалентность 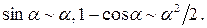
Задача 14. Найти асимптоты графика функции
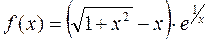 .
.
Решение. Различают вертикальные, горизонтальные и наклонные асимптоты (правда, горизонтальные можно считать частным случаем наклонных).
Прямая 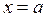 является вертикальной асимптотой, если хотя бы один из односторонних пределов функции в точке
является вертикальной асимптотой, если хотя бы один из односторонних пределов функции в точке 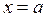 равен
равен 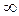 , т.е. вертикальные асимптоты проходят через точки разрыва 2го рода. Данная функция является элементарной и единственной точкой разрыва является точка
, т.е. вертикальные асимптоты проходят через точки разрыва 2го рода. Данная функция является элементарной и единственной точкой разрыва является точка 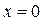 , которая не принадлежит
, которая не принадлежит 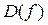 . Вычислим
. Вычислим 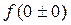 :
:
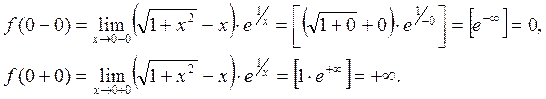
Правый предел функции бесконечен, следовательно, прямая 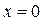 – вертикальная асимптота.
– вертикальная асимптота.
Далее, прямая 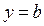 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 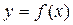 при
при 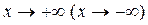 , если существует конечный предел
, если существует конечный предел
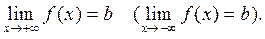
Для упрощения вычисления пределов запишем данную функцию следующим образом:
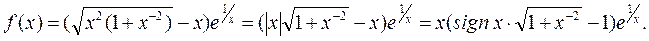
При вычислении пределов пользуемся эквивалентностью для степенной функции и тем фактом, что 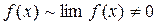 . Имеем:
. Имеем:
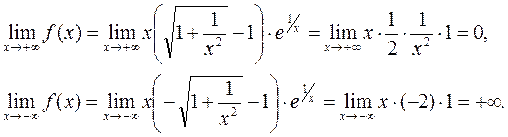
Итак, прямая 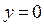 – горизонтальная асимптота при
– горизонтальная асимптота при 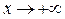 . При
. При 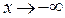 горизонтальной асимптоты нет, но может быть наклонная.
горизонтальной асимптоты нет, но может быть наклонная.
Прямая 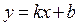 является наклонной асимптотой при
является наклонной асимптотой при 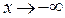 , если существуют конечные пределы
, если существуют конечные пределы
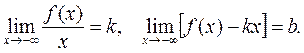
(Аналогичное утверждение справедливо и для 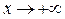 ). Для нашей функции имеем:
). Для нашей функции имеем:
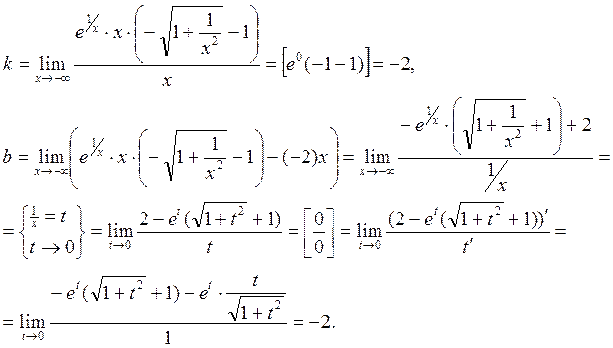
Итак, прямая 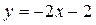 – наклонная асимптота графика данной функции при
– наклонная асимптота графика данной функции при 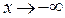 .
.
Ответ: асимптотами графика функции являются прямые 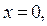
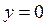 (при
(при 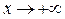 ) и
) и 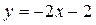 (при
(при 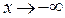 ).
).
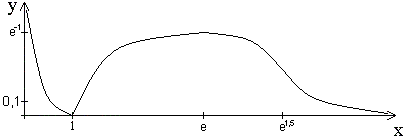
Задача 15. Провести исследование и построить график функции
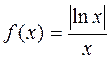 .
.
Решение. Общее исследование функции и построение графика удобно выполнять по следующей схеме:
I. Найти область определение функции, область непрерывности и точки разрыва, вычислить односторонние пределы в точках разрыва, выяснить, не является ли функция четной, нечетной или периодической.
II. Найти асимптоты графика функции.
III. Вычислить производные 1го и 2го порядка и найти критические точки 1го и
2го порядка.
IV. Найти точки экстремума и интервалы возрастания и убывания функции.
V. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции.
VI. Найти точки пересечения графика функции с осями координат.
VII. Построить график функции, используя все полученные результаты исследования.
Заметим, что для большей точности графика рекомендуется находить касательные в точках пересечения графика с осями координат и в точках перегиба, а также односторонние касательные в угловых точках графика (см. ниже).
Руководствуясь указанной схемой, проведем исследование данной функции.
1) Область определения 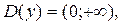 т.к. логарифмы неположительных чисел не существуют. Функция не является ни четной, ни нечетной, ни периодической. Она непрерывна всюду на
т.к. логарифмы неположительных чисел не существуют. Функция не является ни четной, ни нечетной, ни периодической. Она непрерывна всюду на 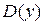 (как элементарная). точка
(как элементарная). точка 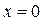 – точка разрыва. Выясним тип разрыва:
– точка разрыва. Выясним тип разрыва:
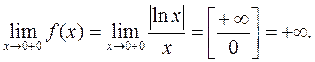
Таким образом,  – точка разрыва 2го рода.
– точка разрыва 2го рода.
2) Полученный в пункте 1) результат позволяет утверждать: прямая 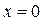 – вертикальная асимптота (единственная). Выясним, имеет ли график горизонтальную асимптоту:
– вертикальная асимптота (единственная). Выясним, имеет ли график горизонтальную асимптоту:
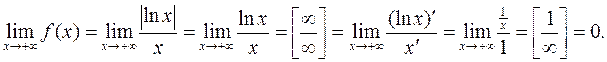
Итак, прямая  (ось абсцисс) – горизонтальная асимптота.
(ось абсцисс) – горизонтальная асимптота.
3) Вычисляем производные, предварительно освободив запись функции от знака модуля:
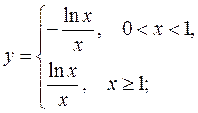
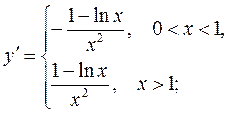
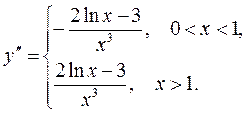
Находим критические точки, т.е. точки из области определения функции, в которых соответствующая производная равна 0 или не существует. Точки 1го порядка:
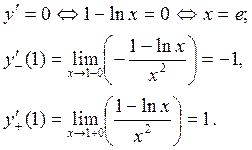
И так как 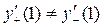 , то
, то 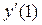 не существует, т.е. точка
не существует, т.е. точка 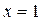 – критическая точка.
– критическая точка.
Точки 2го порядка:
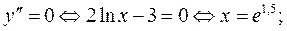
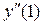 не существует, ибо
не существует, ибо 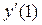 не существует, т.е. точка
не существует, т.е. точка 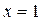 – критическая точка и 2го порядка.
– критическая точка и 2го порядка.
Отметим, что точка графика 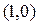 , в которой существует различные односторонние касательные (их угловые коэффициенты равны соответствующим односторонним производным) называется угловой точкой.
, в которой существует различные односторонние касательные (их угловые коэффициенты равны соответствующим односторонним производным) называется угловой точкой.
4-5) Критические точки разбивают область определения на интервалы знакопостоянства производных. Знаки же производных позволяют определить интервалы монотонности и выпуклости-вогнутости, а именно: а) если 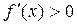 на
на 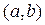 , то
, то 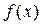 возрастает, если же
возрастает, если же 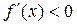 , то
, то 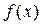 убывает; б) если
убывает; б) если 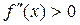 на
на 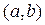 , то график функции направлен выпуклостью вниз, если
, то график функции направлен выпуклостью вниз, если 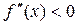 , то выпуклостью вверх.
, то выпуклостью вверх.
Составим сводную таблицу знаков производных. Первая строка изображает 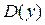 с отмеченными критическими точками как 1го, так и 2го порядка. Во 2й и 3й указаны знаки производных в интервалах, на которые критические точки разбили
с отмеченными критическими точками как 1го, так и 2го порядка. Во 2й и 3й указаны знаки производных в интервалах, на которые критические точки разбили 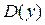 . В 4й строке – графическое изображение поведения функции.
. В 4й строке – графическое изображение поведения функции.
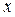 | 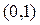 | 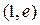 | 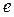 | 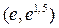 | 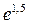 | 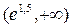 | ||
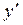 | - | 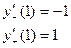 | + | - | - | |||
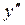 | + | не сущ. | - | - | - | + | ||
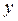 | верт. ас. | 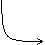 | 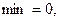 перегиб перегиб 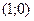 |  | 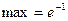 |  | перегиб 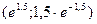 |  |
Анализ показывает, что функция убывает в интервалах  и
и 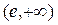 , и возрастает в интервале
, и возрастает в интервале 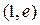 ;
; 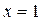 – точка минимума,
– точка минимума, 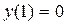 , а
, а 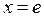 – точка максимума,
– точка максимума, 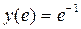 . Далее, график функции является выпуклым вниз на интервалах
. Далее, график функции является выпуклым вниз на интервалах 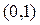 и
и 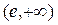 , и выпуклым вверх на интервале
, и выпуклым вверх на интервале 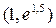 ; точки графика
; точки графика 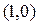 и
и 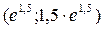 – точки перегиба.
– точки перегиба.
6) График не пересекается с осью 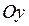 , ибо
, ибо 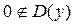 . Чтобы найти точки пересечения графика с осью
. Чтобы найти точки пересечения графика с осью 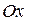 , надо решить уравнение
, надо решить уравнение 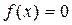 . Для нашей функции:
. Для нашей функции:
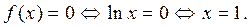
7) Строим эскиз графика
 2015-05-18
2015-05-18 2272
2272
