Кинетическая энергия вращающегося тела

Кинетическая энергия материальной точки 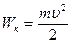. Кинетическая энергия sis материальных точек 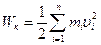. Т.к. 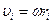, получим выражение кинетической энергии вращения:

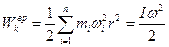
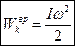(26)

При плоском движении (цилиндр скатывается по наклонной плоскости) полная скорость равна:

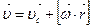, (27)

где 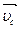- скорость центра масс цилиндра.

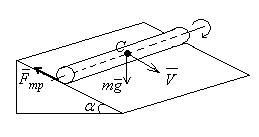
Полная 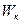равна сумме кинетической энергии поступательного движения его центра масс и кинетической энергии вращательного движения тела относительно центра масс, т.е.:

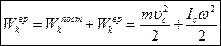(28)

Заключение:

А теперь, рассмотрев весь лекционный материал, подведем итог, сопоставим величины и уравнения вращательного и поступательного движения тела:

Поступательное движение	Вращательное движение
Масса	m	Момент инерции	I
Путь	S	Угол поворота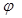
Скорость		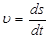Угловая скорость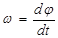
Импульс		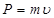Момент импульса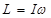
Ускорение		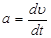Угловое ускорение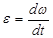
Равнодействующая внешних сил	F	Сумма моментов внешних сил	M
Основное уравнение динамики		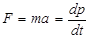Основное уравнение динамики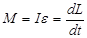
Работа	Fds	Работа вращения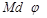
Кинетическая энергия		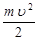Кинетическая энергия вращения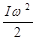

Приложение 1:

Пример:

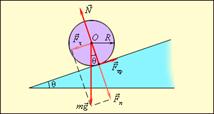
Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения n ₁=0,5 c^-1. Момент инерции j_o тела человека относи-

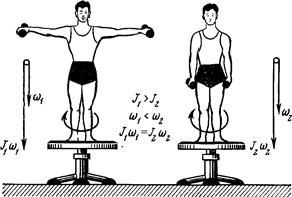
Рис. 3.5

тельно оси вращения равен 1,6 кг м². В вытянутых в стороны руках человек держит по гире массой m =2 кг каждая. Расстояние между гирями l ₁=l,6 м. Опре­делить частоту вращения n ₂, скамьи с человеком, когда он опустит руки и расстояние l ₂ между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.

II.