2015-02-04
426
Рассмотрим замкнутую систему частиц. Замкнутость означает, что воздействие внешних сил на частицы системы пренебрежимо мало. В силу однородности пространства перемещение всех частиц системы на одинаковый отрезок δr не должно изменить механические свойства системы – функция Лагранжа должна сохранить своё прежнее значение. Для незамкнутой системы такой перенос вызвал бы изменение расположения частиц по отношению к взаимодействующим с ними телам, что отразилось бы на механических свойствах системы. Т. о. только для замкнутой системы частиц можно утверждать, что параллельный перенос системы как целого не сопровождается изменением функции L(δL=0).
Полагая перемещение δr очень малым, можно написать
δL=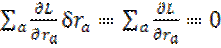 
(9.1)
α – номер частицы
Мы воспользовались тем обстоятельством, что перемещения частиц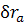 
одинаковы и равны δr.
По предположению δr≠0, поэтому из 9.1 вытекает, что
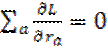(9.2)
В соответствии с уравнениями Лагранжа можно написать
= 
= 
= 
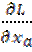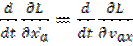
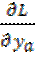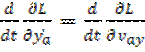
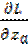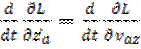
Умножив первое из этих уравнений на орт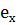 
, второе на орт 
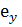, третье на орт 
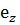и сложив их вместе получим соотношение
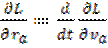(9.3)
Таким образом, уравнению 9.2 можно придать вид
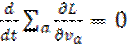(9.4)
Величина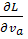 
есть вектор с компонентами
, 
, 
.
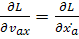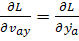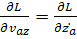Согласно 4.17 эти произведения суть проекции на координатные оси обычного импульса р частицы с номером α. Следовательно
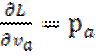(9.5)
С учётом этого обстоятельства уравнение 9.4 запишется следующим образом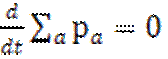 
.
Отсюда вытекает, что
р =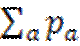 
= const.
Где р – суммарный импульс системы.
Итак исходя из однородности пространства мы пришли к закону: суммарный импульс замкнутой системы частиц остаётся постоянным. Следовательно, импульс замкнутой системы есть так же интеграл движения.
